Cho hàm số $y=x\tan x$. Chứng minh: ${{x}^{2}}y''=2\left( {{x}^{2}}+{{y}^{2}} \right)\left( 1+y \right)$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


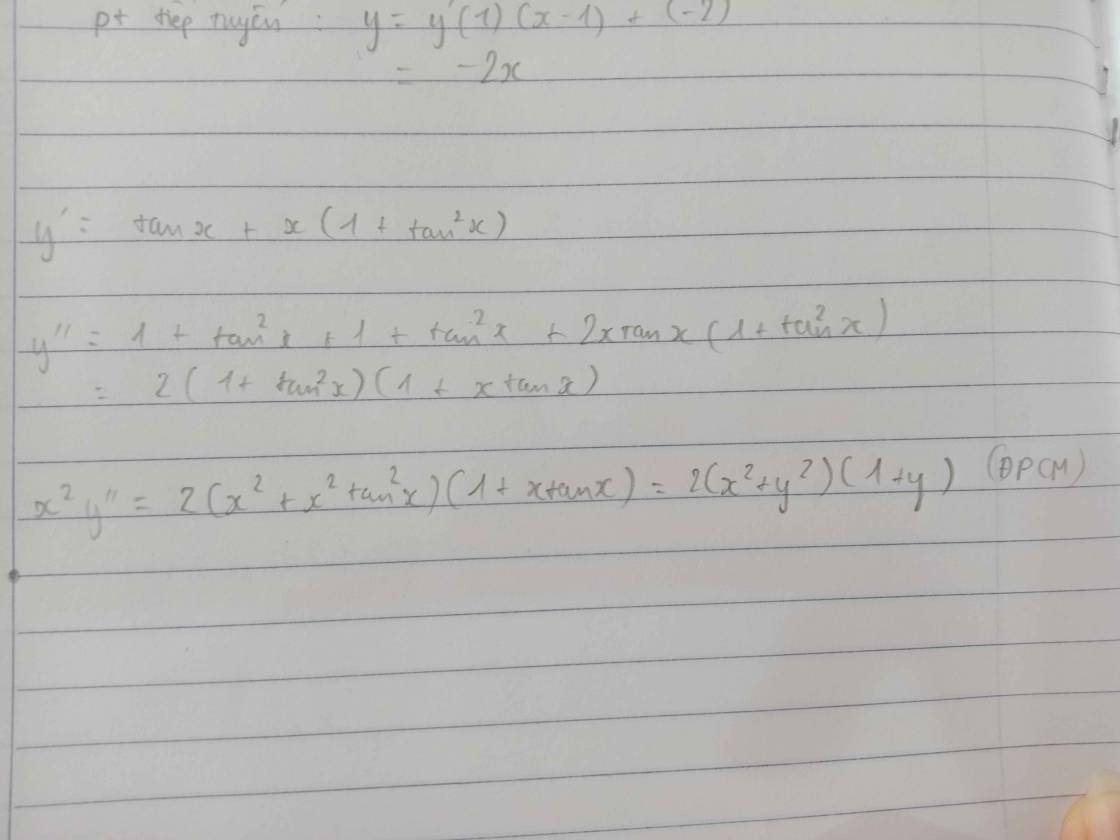

\(y'=\tan x+\frac{x}{\cos^2x}\)
\(y''=\frac{1}{\cos^2x}+\frac{\cos^2-x.2\cos x.\left(-\sin x\right)}{\cos^4x}=\frac{2\cos^2x+2x.\sin x.\cos x}{\cos^4x}\)
\(VT=\frac{2x^2\left(\cos^2x+x\sin x.\cos x\right)}{\cos^4x}\)
\(VP=2\left(x^2+x^2\tan^2x\right)\left(1+x\tan x\right)\)
\(=\frac{2x^2\left(1+x\tan x\right)}{\cos^2x}=\frac{2x^2\left(\cos^2x+x\sin x.\cos x\right)}{\cos^4x}=VT\)

\(y'=\dfrac{\left(x+\sqrt{1+x^2}\right)'}{2\sqrt{x+\sqrt{1+x^2}}}=\dfrac{1+\dfrac{x}{\sqrt{1+x^2}}}{2\sqrt{x+\sqrt{1+x^2}}}\)
\(\Rightarrow2\sqrt{1+x^2}.y'=\dfrac{2\sqrt{1+x^2}\left(1+\dfrac{x}{\sqrt{1+x^2}}\right)}{2\sqrt{x+\sqrt{1+x^2}}}\)
\(=\dfrac{\sqrt{1+x^2}+x}{\sqrt{x+\sqrt{1+x^2}}}=\sqrt{x+\sqrt{1+x^2}}=y\) (đpcm)

Với x 1 , x 2 là hai giá trị bất kì của x thuộc R, ta có:
y 1 = f( x 1 ) = 4 - 2/5 x 1 ; y 2 = f( x 2 ) = 4 - 2/5 x 2
Nếu x 1 < x 2 thì x 1 - x 2 < 0. Khi đó ta có:
y 1 - y 2 = (4 - 2/5 x 1 ) - (4 - 2/5 x 2 )
= (-2)/5( x 1 - x 2 ) > 0. Suy ra y 1 > y 2
Vậy hàm số đã cho là hàm nghịch biến trên R.

Ta có :
f(-x) = 2 . ( -x )2 = 2x2
Mà f(x) = 2x2
Vậy f(-x) = f(x)

a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \tan \left( { - x} \right) = - \tan x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \tan x\) là hàm số lẻ.
b)
\(x\) | \( - \frac{\pi }{3}\) | \( - \frac{\pi }{4}\) | \( - \frac{\pi }{6}\) | \(0\) | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) |
\(\tan x\) | \( - \sqrt 3 \) | \( - 1\) | \( - \frac{{\sqrt 3 }}{3}\) | \(0\) | \(\frac{{\sqrt 3 }}{3}\) | \(1\) | \(\sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \tan x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\).

