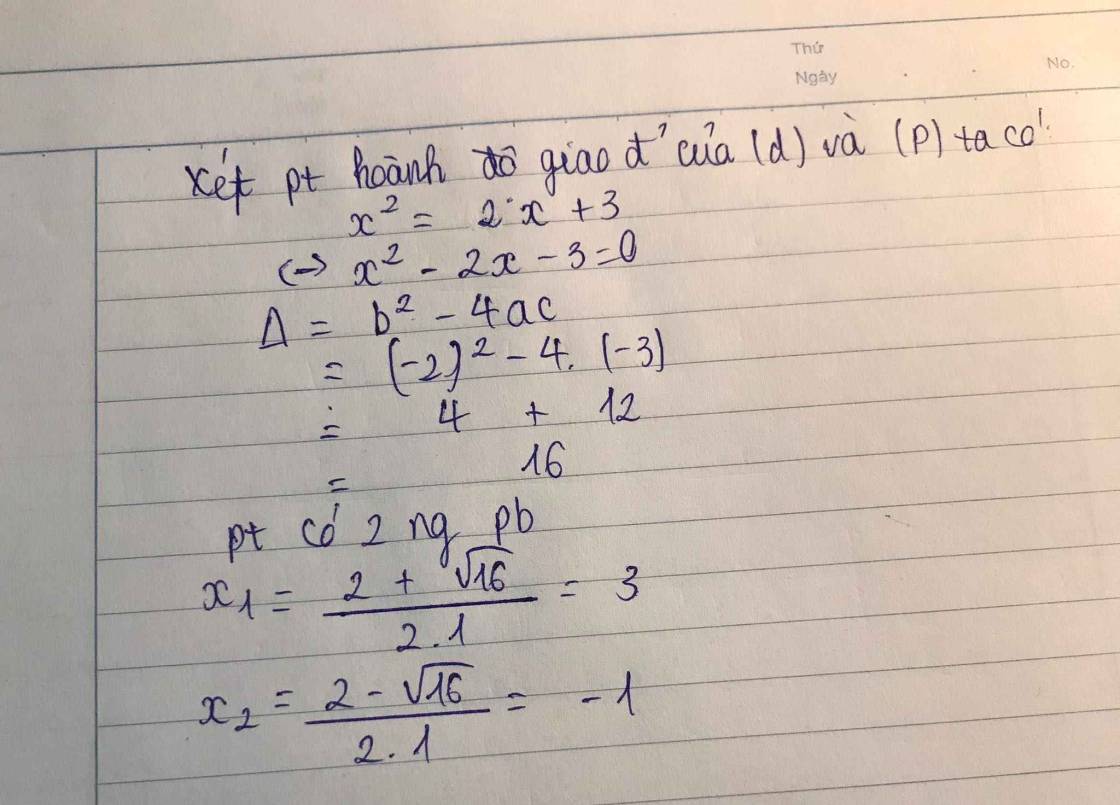Trong mặt phẳng tọa độ $O x y$ cho parabol $(P): y=x^{2}$ và đường thẳng $(d): y=m x+3$.
a) Tìm tọa độ giao điểm của đường thẳng $(d)$ và parabol $(P)$ với $m=2$.
b) Chứng minh $(d)$ luôn cắt $(P)$ tại hai điểm phân biệt. Gọi hai giao điểm lần lượt là $A\left(x_{1} ; y_{1}\right)$ và $B\left(x_{2} ; y_{2}\right)$. Tìm $m$ để $y_{1}+y_{2}=4\left(x_{1}+x_{2}\right)+3$.