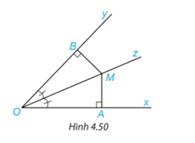
Vẽ góc xOy và Oz là tia phân giác của góc xOy, trên tia Oz lấy điểm M. Vẽ MA vuông góc với Oy, vẽ MB vuông góc với Oy. Chứng minh MA = MB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SS
10 tháng 2 2022
Vì Oz là tia phân giác của góc xOy
=>góc AOM = góc BOM
VÌ MA\(\perp\)Ox =>góc MAO=90o
MB \(\perp\)Oy =>góc MBO=90o
Xét \(\Delta AOM\)và \(\Delta BOM\)có:
Góc MAO= Góc MBO(Cùng bằng 90o)
OM:cạnh chung
Góc AOM = góc BOM
=>\(\Delta AOM=\Delta BOM\left(Ch-gn\right)\)
=>MA=MB(các cạnh tương ứng)
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
1 tháng 3 2022
Xét ΔOAM và ΔOBM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔOAM=ΔOBM
Suy ra: MA=MB
Xét ΔOKM vuông tại K và ΔOHM vuông tại H có
OM chung
\(\widehat{KOM}=\widehat{HOM}\)
Do đó;ΔOKM=ΔOHM
Suy ra: OH=OK
=>AH=BK
Xét ΔMAH vuông tại H và ΔMBK vuông tại K có
MA=MB
AH=BK
Do đó: ΔMHA=ΔMKB
Xét △AOM và △BOM
Ta cs: OM cạnh chung
góc O1 = góc O2
góc A = góc B = 90 độ
vậy △AOM = △BOM ( chgn )
=> AM = BM ( cặp cạnh tương ứng )