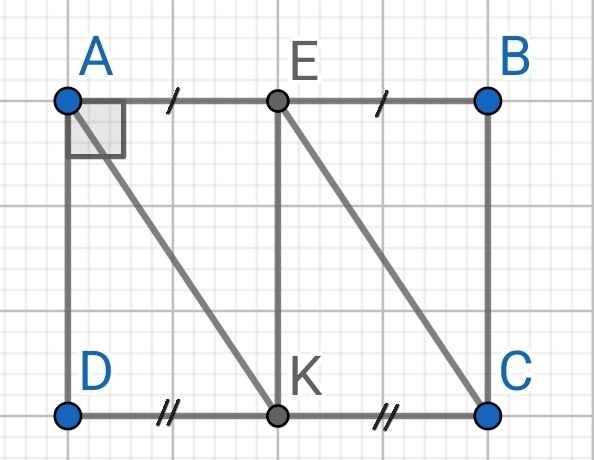
a) Cho hbh ABCD. Gọi M là trung điểm CD; N là điểm thuộc AD sao cho 3AN=AD. Gọi G là trọng tâm tam giác BMN, đường thẳng AG cắt BC tại K. Tính tỉ số \(\dfrac{BK}{BC}\)
b) Trong mp tọa độ Oxy, cho tam giác ABC cân tại C và có diện tích bằng 10. Đường thẳng AB có pt x-2y=0. Điểm I(4;2) là trung điểm AB, điểm \(M\left(4;\dfrac{9}{2}\right)\) thuộc đường thẳng BC. Tìm tọa độ A,B,C biết B có tung độ là số nguyên