hình bình hành ABCD I thuộc AC từ I kẻ FiE bất kì E thuộc AB F thuộc DC từ I kẻ GH bất kì G thuộc AD H thuộc BC chứng minh GE // FH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 4 2017
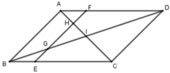
Có ABCD là hình bình hành nên: AD // BC, AB // DC
Xét ΔBGE và ΔDGF có:
B G E ^ = D G F ^ (đối đỉnh)
E B G ^ = F D G ^ (so le trong)
=> ΔBGE ~ ΔDGF (g-g) nên C đúng
Xét ΔAHF và ΔCHE có:
A H F ^ = C H E ^ (đối đỉnh)
H A F ^ = H C E ^ (so le trong)
=> ΔAHF ~ ΔCHE (g-g) nên D đúng
Lại có GH // AB ⇒ I H G ^ = I A B ^ (đồng vị)
Xét ΔGHI và ΔBAI có
Chung I
I H G ^ = I A B ^ (cmt)
=> ΔGHI ~ ΔBAI (g-g)
Suy ra B đúng
Chỉ có A sai.
Đáp án A
31 tháng 10 2021
Vì ME//AC và MF//AB nên AEMF là hbh
Mà I là trung điểm AM nên I là trung điểm EF
Do đó E đx F qua I
18 tháng 12 2023
a: Xét ΔGAB có KC//AB
nên \(\dfrac{GC}{GB}=\dfrac{GK}{GA}\)
b: Xét ΔKAD và ΔAGB có
\(\widehat{KAD}=\widehat{AGB}\)(hai góc so le trong, DA//BC)
\(\widehat{AKD}=\widehat{GAB}\)(hai góc so le trong, DK//AB)
Do đó: ΔKAD đồng dạng với ΔAGB
=>\(\dfrac{AK}{AG}=\dfrac{AD}{GB}\)
=>\(\dfrac{AK}{AD}=\dfrac{AG}{GB}\)
=>\(\dfrac{AD}{AK}=\dfrac{BG}{GA}\)