Cho tam giác ABC đồng dạng tam giác MNP tương ứng ∠𝐴 = ∠𝑀, ∠𝐵 = ∠𝑁. Kẻ các đường trung tuyến AE và MF của hai tam giác. (𝐸 ∈ 𝐵𝐶; 𝐹 ∈ 𝑁𝑃).
a. Chứng minh rằng tam giác AEB đồng dạng tam giác MFN.
b. Cho biết tỷ số đồng dạng 𝐴𝐵 𝑀𝑁 = 𝑘. Chứng minh rằng 𝐴𝐸 = 𝑘. 𝑀𝐹.


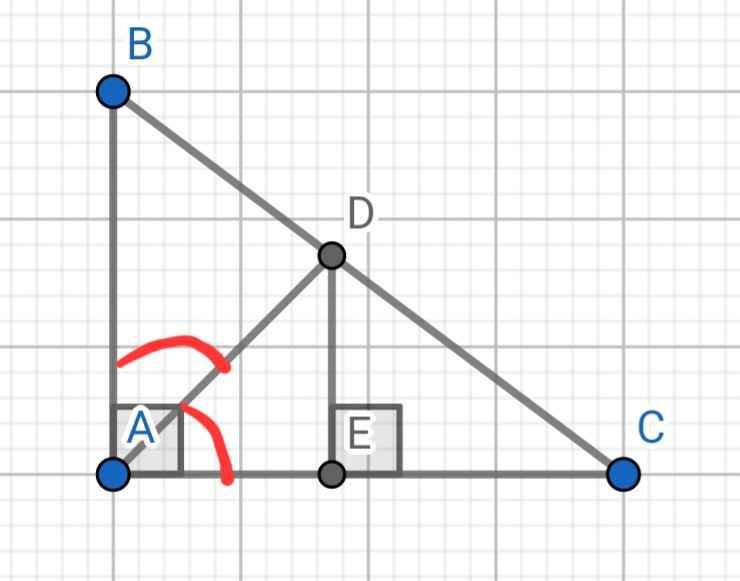
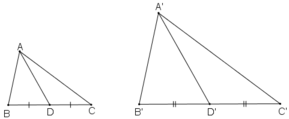
 ΔABC theo tỉ số k
ΔABC theo tỉ số k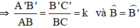
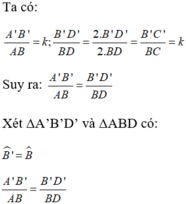
 ΔABD theo tỉ số k.
ΔABD theo tỉ số k.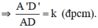
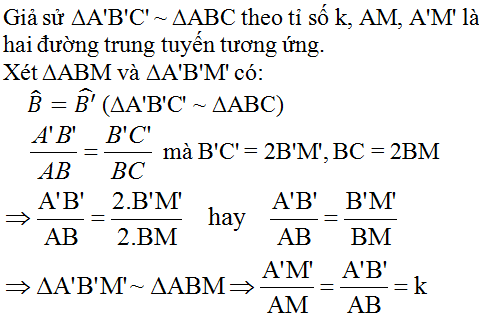
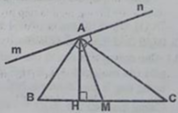

a: ΔABC đồng dạng với ΔMNP
=>AB/MN=BC/NP=AC/MP và góc B=góc N
=>AB/MN=BE/NF và góc B=góc N
Xét ΔABE và ΔMNF có
AB/MN=BE/NF
góc B=góc N
=>ΔABE đồng dạng với ΔMNF
b: ΔABE đồng dạng với ΔMNF
=>AB/MN=AE/MF=k
=>AE=k*MF