Bài 1 : Tìm x biết : ( x ϵ N )
a) 25 < 3x < 250
b) ( 2x + 1 )3 = 125
c) 100 < 52x - 1 < 56
d) x15 = x
e) ( x - 5 )4 = ( x - 5 )6
g) 32x + 2 = 95 - x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,
\(\left(5x+3\right)^2=\dfrac{25}{9}\\ \Rightarrow\left[{}\begin{matrix}5x+3=\dfrac{5}{3}\\5x+3=-\dfrac{5}{3}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{4}{15}\\x=-\dfrac{7}{6}\end{matrix}\right.\)
b,
\(\left(-\dfrac{1}{2}x+3\right)^3=-\dfrac{1}{125}\\ \Rightarrow-\dfrac{1}{2}x+3=-\dfrac{1}{5}\\ \Rightarrow x=\dfrac{32}{5}\)
c,

Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau: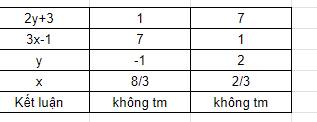
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.

a,Do (2x + 1)( 3x +4) = 21 nên 21 chia hết cho 3x + 4 suy ra 3x + 4 thuộc Ư(21)= (1;3;7;14;21)
- Với 3x + 4 = 1 suy ra 3x không thuộc N ( loại)
- Với 3x + 4 = 3 suy ra 3x không thuộc N ( loại )
-Với 3x + 4 =7 suy ra 3x =3 suy ra x=1 , 2x+1 = 3 suy ra x=1
- Với 3x +4 =14 suy ra 3x = 10 suy ra x không thuộc N (loại)
- Với 3x +4 = 21 suy ra 3x = 17 suy ra x không thuộc N (loại)
Vậy x = 1.
b, Do ( 2x-2)(4y+3) =14 suy ra (4y+3) thuộc Ư(14) =(1;2;7;14)
- Với (4y+3) =1 suy ra 4y không thuộc N( loại)
-Với (4y+3) =2 suy ra 4y không thuôc N (loại)
-Với (4y+3) =7 suy ra 4y =4 suy ra y=1, do đó (2x-2) = 2 suy ra x=2
-Với (4y+3) =14 suy ra 4y =11 suy ra y không thuộc N ( loại)
Vậy (x;y) = (2;1)

2:
a: =>2(x+1)=26
=>x+1=13
=>x=12
b: =>(6x)^3=125
=>6x=5
=>x=5/6(loại)
c: =>\(7\cdot3^x\cdot\dfrac{1}{3}+11\cdot3^x\cdot3=318\)
=>3^x=9
=>x=2
d: -2x+13 chia hết cho x+1
=>-2x-2+15 chia hết cho x+1
=>15 chia hết cho x+1
=>x+1 thuộc {1;3;5;15}
=>x thuộc {0;2;4;14}
e: 4x+11 chia hết cho 3x+2
=>12x+33 chia hết cho 3x+2
=>12x+8+25 chia hết cho 3x+2
=>25 chia hết cho 3x+2
=>3x+2 thuộc {1;-1;5;-5;25;-25}
mà x là số tự nhiên
nên x=1
1:
a: Đặt A=2^2024-2^2023-...-2^2-2-1
Đặt B=2^2023+2^2022+...+2^2+2+1
=>2B=2^2024+2^2023+...+2^3+2^2+2
=>B=2^2024-1
=>A=2^2024-2^2024+1=1
c: \(=\dfrac{3^{12}\cdot2^{11}+2^{10}\cdot3^{12}\cdot5}{2^2\cdot3\cdot3^{11}\cdot2^{11}}=\dfrac{2^{10}\cdot3^{12}\left(2+5\right)}{2^{13}\cdot3^{12}}\)
\(=\dfrac{7}{2^3}=\dfrac{7}{8}\)

Bài `1:`
`a)3x^3+6x^2=3x^2(x+2)`
`b)x^2-y^2-2x+2y=(x-y)(x+y)-2(x-y)=(x-y)(x+y-2)`
Bài `2:`
`a)(2x-1)^2-25=0`
`<=>(2x-1-5)(2x-1+5)=0`
`<=>(2x-6)(2x+4)=0`
`<=>[(x=3),(x=-2):}`
`b)Q.(x^2+3x+1)=x^3+2x^2-2x-1`
`<=>Q=[x^3+2x^2-2x-1]/[x^2+3x+1]`
`<=>Q=[x^3-x^2+3x^2-3x+x-1]/[x^2+3x+1]`
`<=>Q=[(x-1)(x^2+3x+1)]/[x^2+3x+1]=x-1`

Bài 2:
a: Ta có: \(A=\left(x+1\right)^3+\left(x-1\right)^3\)
\(=x^3+3x^2+3x+1+x^3-3x^2+3x-1\)
\(=2x^3+6x\)
b: Ta có: \(B=\left(x-3\right)^3-\left(x+3\right)\left(x^2-3x+9\right)+\left(3x-1\right)\left(3x+1\right)\)
\(=x^3-9x^2+27x-27-x^3-27+9x^2-1\)
\(=27x-55\)

a) \(2^x\cdot4=128\)
\(\Rightarrow2^x\cdot2^2=2^7\)
\(\Rightarrow2^{x+2}=2^7\)
\(\Rightarrow x+2=7\)
\(\Rightarrow x=5\)
b) \(\left(2x+1\right)^3=125\)
\(\Rightarrow\left(2x+1\right)^3=5^3\)
\(\Rightarrow2x+1=5\)
\(\Rightarrow2x=4\)
\(\Rightarrow x=4:2\)
\(\Rightarrow x=2\)
c) \(2x-2^6=6\)
\(\Rightarrow2x-64=6\)
\(\Rightarrow2x=70\)
\(\Rightarrow x=70:2\)
\(\Rightarrow x=35\)
d) \(64\cdot4^x=45\)
\(\Rightarrow4^3\cdot4^x=45\)
\(\Rightarrow4^{x+3}=45\)
Xem lại đề
e) \(27\cdot3^x=243\)
\(\Rightarrow3^3\cdot3^x=3^5\)
\(\Rightarrow3^{x+3}=3^5\)
\(\Rightarrow x+3=5\)
\(\Rightarrow x=2\)
g) \(49\cdot7^x=2401\)
\(\Rightarrow7^2\cdot7^x=7^4\)
\(\Rightarrow7^{x+2}=7^4\)
\(\Rightarrow x+2=4\)
\(\Rightarrow x=2\)
h) \(3^x=81\)
\(\Rightarrow3^x=3^4\)
\(\Rightarrow x=4\)
k) \(3^4\cdot3^x=3^7\)
\(\Rightarrow3^{x+4}=3^7\)
\(\Rightarrow x+4=7\)
\(\Rightarrow x=3\)
n) \(3^x+25=26\cdot2^2+2\cdot3^0\)
\(\Rightarrow3^x+25=104+2\)
\(\Rightarrow3^x+25=106\)
\(\Rightarrow3^x=81\)
\(\Rightarrow3^x=3^4\)
\(x=4\)
`@` `\text {Ans}`
`\downarrow`
`a)`
`2^x*4 = 128`
`=> 2^x = 128 \div 4`
`=> 2^x = 2^7 \div 2^2`
`=> 2^x = 2^5`
`=> x = 5`
Vậy, `x = 5.`
`b)`
\(\left(2x+1\right)^3=125\)
`=> (2x + 1)^3 = 5^3`
`=> 2x + 1 = 5`
`=> 2x = 5-1`
`=> 2x = 4`
`=> x = 4 \div 2`
`=> x = 2`
Vậy, `x = 2`
`c)`
\(2x-2^6=6\)
`=> 2x = 6+2^6`
`=> 2x = 70`
`=> x = 70 \div 2`
`=> x = 35`
Vậy, `x = 35`
`d)`
\(64\cdot4^x=45\) Bạn xem lại đề
`e)`
`27*3^x = 243`
`=> 3^3 * 3^x = 3^5`
`=> 3^(3 + x) = 3^5`
`=> 3 + x = 5`
`=> x = 5 - 3`
`=> x = 2`
Vậy, `x = 2`
`g)`
`49* 7^x = 2401`
`=> 7^2 * 7^x = 7^4`
`=> 7^(2 + x) = 7^4`
`=> 2 + x = 4`
`=> x = 4 - 2`
`=> x = 2`
Vậy, `x = 2`
`h)`
`3^x = 81`
`=> 3^x = 3^4`
`=> x = 4`
Vậy, `x = 4`
`k)`
`3^4 * 3^x = 3^7`
`=> 3^(4 + x) = 3^7`
`=> 4 + x = 7`
`=> x = 7 - 4`
`=> x = 3`
Vậy, `x = 3`
`n)`
`3^x + 25 = 26*2^2 + 2*3^0`
`=> 3^x + 25 = 104 + 2`
`=> 3^x + 25 = 106`
`=> 3^x = 106 - 25`
`=> 3^x = 81`
`=> 3^x = 3^4`
`=> x = 4`
Vậy, `x = 4.`
\(#48Cd\)
\(x^{15}=x\Rightarrow\hept{\begin{cases}x=0\\x=1\end{cases}}\)
tíc mình nha
\(\left(2x+1\right)^3=125\)
\(\Rightarrow\left(2x+1\right)^3=5^3\)
\(\Rightarrow2x+1=5\)
\(\Rightarrow2x=4\Rightarrow x=2\)
tíc mình nha