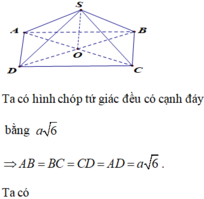
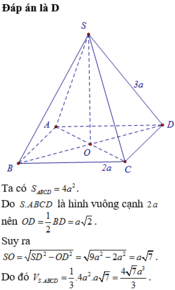
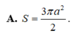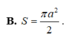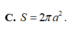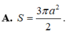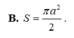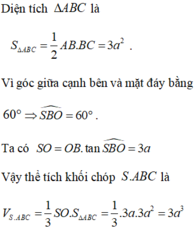tính dtxq và dttp của hình chóp tứ giác đều có cạnh đáy bằng cạnh bên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 9 2018
Gọi O là tâm hình vuông của mặt đáy. Khi đó O cũng là tâm của mặt cầu. Ta có:
R 2 = S O 2 = a 2 - a 2 2 2 = a 2 2 S = 4 πR 2 = 2 πa 2
Đáp án C
CM
28 tháng 2 2019
Chọn đáp án A
Gọi O là giao điểm của AC và BD.
Áp dụng định lí Pytago vào tam giác vuông ABC có:
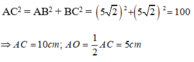
Áp dụng định lí Pytago vào tam giác vuông SAO có:
S O 2 = S A 2 - A O 2 = 13 2 - 5 2 = 144 nên SO = 12cm
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
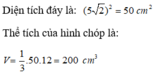
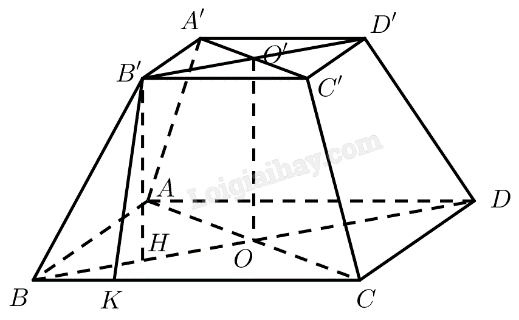
Gọi \(O\) và \(O'\) lần lượt là tâm của hai đáy.
Kẻ \(B'H \bot B{\rm{D}}\left( {H \in B{\rm{D}}} \right),B'K \bot BC\left( {K \in BC} \right)\)
\(\begin{array}{l}B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = 2a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = a\sqrt 2 \\B'D' = \sqrt {A'B{'^2} + A'{\rm{D}}{{\rm{'}}^2}} = a\sqrt 2 \Rightarrow B'O' = \frac{1}{2}B'{\rm{D'}} = \frac{{a\sqrt 2 }}{2}\end{array}\)
\(OO'B'H\) là hình chữ nhật \( \Rightarrow OH = B'O' = \frac{{a\sqrt 2 }}{2},B'H = OO' = a\)
\( \Rightarrow BH = BO - OH = \frac{{a\sqrt 2 }}{2}\)
Tam giác \(BB'H\) vuông tại \(H\) có: \(BB' = \sqrt {B'{H^2} + B{H^2}} = \frac{{a\sqrt 6 }}{2}\)
\(BCC'B'\) là hình thang cân \( \Rightarrow BK = \frac{{BC - B'C'}}{2} = \frac{a}{2}\)
Tam giác \(BB'K\) vuông tại \(K\) có: \(B'K = \sqrt {BB{'^2} - B{K^2}} = \frac{{a\sqrt 5 }}{2}\)