tìm x y nguyên biết \(2^x-3^y=7\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 2 2020
Các bạn giúp mình giải với nhé! Đúng thì mình k đúng nhé. Cảm ơn các bạn nhiều lắm. Yêu cả nhà.
28 tháng 2 2021
\(1.\left(x-5\right)^{23}.\left(y+2\right)^7=0\)
\(\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0\\\left(y+2\right)^7=0\end{cases}\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0^{23}\\\left(y+2\right)^7=0^7\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x-5=0\\y+2=0\end{cases}\Rightarrow\hept{\begin{cases}x=0+5\\y=0-2\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x=5\\y=-2\end{cases}}\)
Vậy \(\left(x;y\right)=\left(5;-2\right)\)
9 tháng 1 2022
Bài 1:
Để E nguyên thì \(x+5⋮x-2\)
\(\Leftrightarrow x-2\in\left\{1;-1;7;-7\right\}\)
hay \(x\in\left\{3;1;9;-5\right\}\)
NH
1
KV
12 tháng 11 2023
Bài 1
a) (x + 3)(x + 2) = 0
x + 3 = 0 hoặc x + 2 = 0
*) x + 3 = 0
x = 0 - 3
x = -3 (nhận)
*) x + 2 = 0
x = 0 - 2
x = -2 (nhận)
Vậy x = -3; x = -2
b) (7 - x)³ = -8
(7 - x)³ = (-2)³
7 - x = -2
x = 7 + 2
x = 9 (nhận)
Vậy x = 9
30 tháng 7 2023
a,x.y=3=1x3=3x1=-1x(-3)=-3x(-1).
Vậy (x,y)=(1,3)=(3,1)=(-1,-3)=(-3,-1)
b,x.(y+1)=5=1x5=5x1=-1x(-5)=-5x(-1)
=>
| x | 1 | 5 | -1 | -5 |
| y+1 | 5 | 1 | -5 | -1 |
| y | 4 | 0 | -6 | -2 |
Vậy (x,y)=(1,4)=(5,0)=(-1,-6)=(-1,-2).
c,(x-2)(y+3)=7=1x7=7x1=-1x(-7)=-7(-1)
=>
| x-2 | 1 | 7 | -1 | -7 |
| y+3 | 7 | 1 | -7 | -1 |
| x | 3 | 9 | 1 | -5 |
| y | 4 | -2 | -10 | -4 |
Vậy (x,y)=(3,4)=(9,-2)=(1,-10)=(-5,-4).
MT
1
VT
0
PT
2
LB
6 tháng 5 2017
Ta có
\(\frac{x-3}{3}=\frac{7}{y+2}\)
\(\Rightarrow\left(x-3\right).\left(y+2\right)=3.7=21\)
Mà \(21=1.21;-1.-21;21.1;-21.-1;7.3;-7.-3\)
\(\Rightarrow\)Từng trường hợp rồi giải ra nhé
SN
1
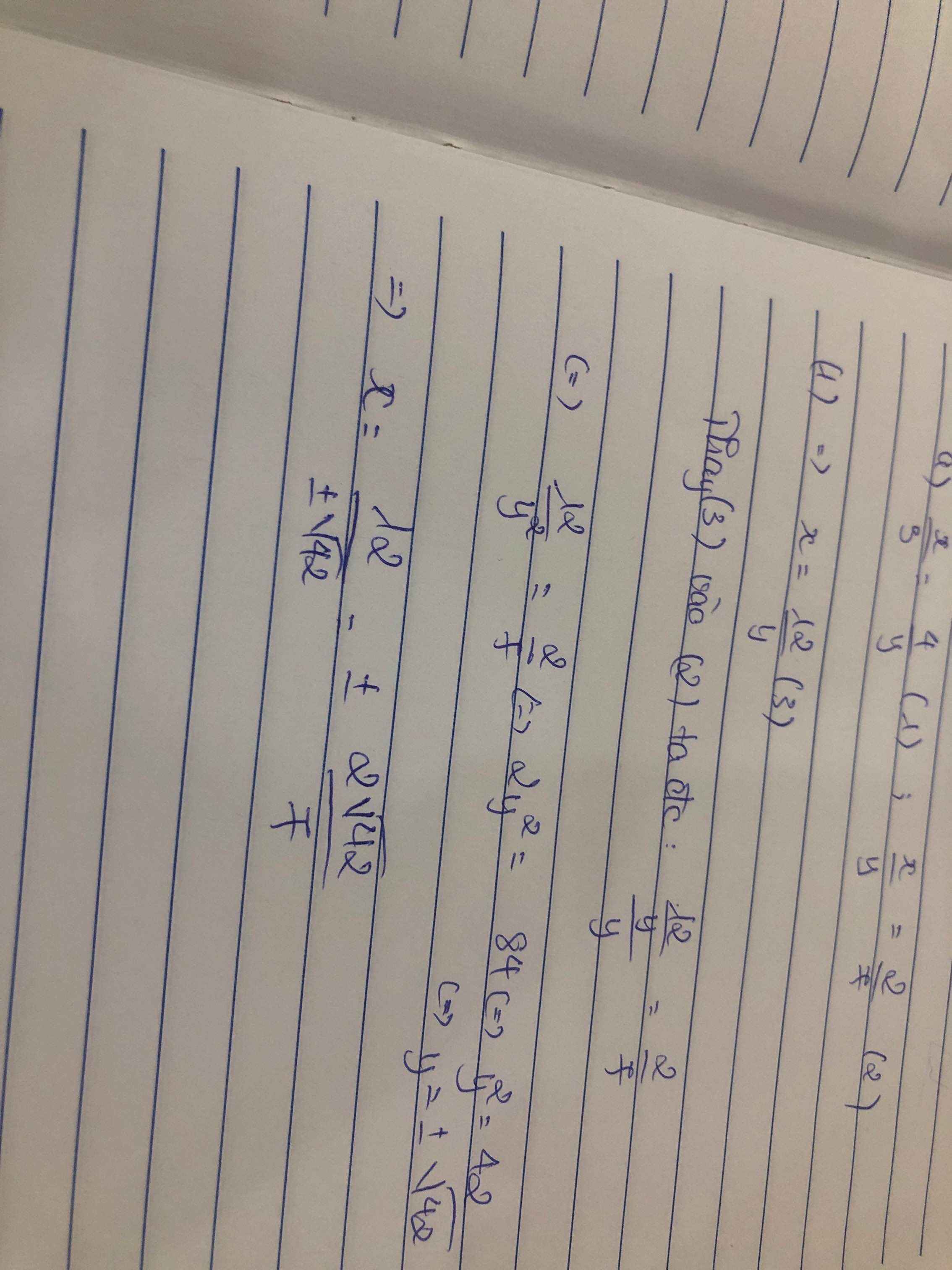
Lời giải:
Dễ thấy $x,y$ không âm và $x\geq 3$
Nếu $y=0$ thì $x=3$ (thỏa mãn)
Nếu $y\geq 1$:
$2^x=3^y+7\equiv 1\pmod 3$
$\Leftrightarrow (-1)^x\equiv 1\pmod 3\Rightarrow x$ chẵn.
Với $x\geq 3$ thì $3^y=2^x-7\equiv 1\pmod 4$
$\Leftrightarrow (-1)^y\equiv 1\pmod 4\Rightarrow y$ chẵn.
Đặt $x=2a; y=2b$ với $a,b$ là số tự nhiên.
Khi đó: $(2^a-3^b)(2^a+3^b)=7$
$\Rightarrow 2^a-3^b=1; 2^a+3^b=7$
$\Rightarrow 2^{a+1}=8\Rightarrow a=2$ kéo theo $b=1$
$\Rightarrow x=4; y=2$
Vậy $(x,y)=(3,0); (4,2)$