Cho tam giác ABC, M là trung điểm của BC biết BM = AC. D là điểm đối xứng với B qua A; E là điểm đối xứng voi M qua C.
Chứng minh DM vuông góc CE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 1 2023
a: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
b: Xét tứ giác AEBC có
N là trung điểm chung của AB và EC
nên AEBC là hình bình hành
=>AE//BC và AE=BC
=>AD//AE và AD=AE
=>A là trung điểm của DE
9 tháng 9 2018
Gọi I là trung điểm của BM \(\Rightarrow IM=\frac{1}{2}BM=\frac{1}{2}AC\)(vì BM = AC)
\(\Delta AIC\)có IM là đường trung tuyến ứng với cạnh AC và IM = 1/2 AC
\(\Rightarrow\Delta AIC\)vuông tại I \(\Rightarrow AI\perp IC\) (1)
AI là đường trung bình của \(\Delta DBM\Rightarrow AI//DM\) (2)
IC là đường trung bình của \(\Delta BME\Rightarrow IC//BE\) (3)
Từ (1), (2) và (3) \(\Rightarrow DM\perp BE.\)
Chúc bạn học tốt.
15 tháng 7 2017
Xét tam giác COA tao có FD là đường trung bình
=> FD = 1/2 A'C'
chứng minh tương tự FD = 1/2 AC => A'C' =AC
chứng minh tương tự B'C"= BC; A'B'=AB
vậy tam giác ABC =tam giác A'B'C'
2 tháng 1 2023
a: D đối xứng M qua AB
nên AD=AM; BD=BM và DM vuông góc với AB
Xét tứ giác AIDE có
góc AID=góc AED=góc EAI=90 độ
Do đó: AIDE là hình chữ nhật
b: AD=AM
BD=BM
mà AD=BD
nên AD=AM=BD=BM
=>ADBM là hình thoi
c: AI=AB/2=3cm
AE=AC/2=4,5cm
SAIDE=3*4,5=13,5cm2
CM
2 tháng 8 2019
Hình chữ nhật AEDF trở thành hình vuông khi AE = AF
Ta có: AE = 1/2 AB; AF = 1/2 AC
Nên AE = AF ⇒ AB = AC
Vậy nếu ∆ ABC vuông cân tại A thì tứ giác AEDF là hình vuông.
30 tháng 11 2021
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
CM
19 tháng 1 2017
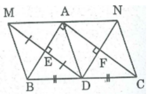
Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD
Hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN
Hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng
Và AM = AN nên A là trung điểm của MN
Vậy điểm M và điểm N đối xứng qua điểm A.