cho A=5x^2y+3xy^2+2yz
B=-5xy^2+2x^2y-2yz+2
Tính A+B bằng 2 cách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nhóm 1:-5x\(^2\)yz;\(\dfrac{2}{3}\)x\(^2\)yz
Nhóm 2:3xy\(^2\)z;-\(\dfrac{2}{3}\)xy\(^2\)z
Nhóm 3:10x\(^2\)y\(^2\)z;\(\dfrac{5}{7}\)x\(^2\)y\(^2\)z

a) 5xy² . (-3y)²
= 5xy² . 9y²
= (5.9).x.(y².y²)
= 45xy⁴
Hệ số: 45
Bậc: 5
b) x²yz . (-2xy)³
= x²yz . (-8x³y³)
= -8.(x².x³).(y.y³).z
= -8x⁵y⁴z
Hệ số: -8
Bậc: 10
c) (-2x²y)².8x³yz³
= 4x⁴y².8x³yz³
= (4.8).(x⁴.x³).(y².y).z³
= 32x⁷y³z³
Hệ số: 32
Bậc: 13
d) (-2xy³)².(-2xyz)³
= 4x²y⁶.(-8x³y³z³)
= [4.(-8)].(x².x³).(y⁶.y³).z³
= -32x⁵y⁹z³
Hệ số: -32
Bậc: 17
e) (-5xy³z).(-4x²)²
= (-5xy³z).(16x⁴)
= (-5.16).(x.x⁴).y³.z
= -80x⁵y³z
Hệ số: -80
Bậc: 9
f) (2x²y³)².(-2xy)
= (4x⁴y⁶).(-2xy)
= [4.(-2)].(x⁴.x).(y⁶.y)
= -8x⁵y⁷
Hệ số: -8
Bậc: 12
a: =5xy^2*9y^2=45xy^4
b: =x^2yz*(-8)x^3y^3=-8x^5y^4z
c: =4x^4y^2*8x^3yz^3=32x^7y^3z^3
d: =4x^2y^6*(-8)x^3y^3z^3=-32x^5y^9z^3
e: =-5xy^3z*16x^4=-80x^5y^3z
f: =4x^4y^6*(-2xy)=-8x^5y^7

a) Các đơn thức đồng dạng trong các đơn thức sau là: \(5x^2yz;-2x^2yz\) ; \(x^2yz\) ; \(0,2x^2yz\)
b) \(M\left(x\right)=3x^2+5x^3-x^2+x-3x-4\)
\(M\left(x\right)=(3x^2-x^2)+5x^3+(x-3x)-4\)
\(M\left(x\right)=2x^2+5x^3-2x-4\)
\(M\left(x\right)=5x^3+2x^2-2x-4\)
c) \(P+Q=\left(x^3x+3\right)+\left(2x^3+3x^2+x-1\right)\)
\(P+Q=x^3x+3+2x^3+3x^2+x-1\)
\(P+Q=\left(x^3+2x^3\right)+\left(x+x\right)+\left(3-1\right)+3x^2\)
\(P+Q=3x^3+2x+2+3x^2\)

a: \(=\left(4xy^2+2xy^2\right)+\left(3x^2y-3x^2y\right)=6xy^2\)
b: \(=xy\left(\dfrac{1}{5}+\dfrac{1}{3}\right)+xy^2\left(\dfrac{4}{3}-\dfrac{2}{5}\right)=\dfrac{8}{15}xy+\dfrac{14}{15}xy^2\)
d: \(=\dfrac{-4}{9}\cdot\dfrac{3}{2}\cdot xy^2\cdot xy^3=-\dfrac{2}{3}x^2y^5\)

Mình viết lại cho dễ đọc.
a) A+ x2+4xy + x2- y2 = 2y +3xy- 5x2y +5x2y + 2x2y2
b) A- ( -2 x3) -y2+ 32x2- 4xy - y = 10z2 + y2z2
c) A= -2x + 5xy - 3x2y + 2x2y2 - 2 y2x
B= xy- 3x2y+ 2x2y + 2x2y2 - 2- y2x

a: A+B=x+2y+x-2y=2x
A-B=x+2y-x+2y=4y
b: A+B
=2x^2y-x^3-xy^2+1+x^3+xy^2-2
=2x^2y-1
A-B
=2x^2y-x^3-xy^2+1-x^3-xy^2+2
=-2x^3+2x^2y-2xy^2+3
c: A+B
=x^2-2yz+z^2+3yz+5x^2-z^2
=6x^2+yz
A-B
=x^2-2yz+z^2-3yz-5x^2+z^2
=-4x^2+2z^2-5yz

`#3107`
`a)`
`A=`\(3x^4 + \dfrac{1}3xyz - 3x^4 - \dfrac{4}3xyz + 2x^2y - 6z\)
`= (3x^4 - 3x^4) + (1/3xyz - 4/3xyz) + 2x^2y - 6z`
`= -xyz + 2x^2y - 6z`
Thay `x = 1; y = 3` và `z = 1/3` vào A
`A = -1*3*1/3 + 2*1^2*3 - 6*1/3`
`= -1 + 6 - 2`
`= 6 - 3`
`= 3`
Vậy, `A=3`
`b)`
`B=`\(4x^3 - \dfrac{2}7xyz - 4x^3 - \dfrac{4}3xyz + 4x^2y\)
`= (4x^3 - 4x^3) + (-2/7xyz - 4/3xyz) + 4x^2y`
`= -34/21 xyz + 4x^2y`
Thay `x = -1; y = 2` và `z = -1/2` vào B
`B = -34/21*(-1)*2*(-1/2) + 4*(-1)^2 * 2`
`= -34/21 + 8`
`= 134/21`
Vậy, `B = 134/21`
`c)`
`C=`\(4x^2 + \dfrac{1}2xyz - \dfrac{2}3xy^2z - 5x^2yz + \dfrac{3}4xyz\)
`= 4x^2 + (1/2xyz + 3/4xyz) - 2/3xy^2z - 5x^2yz `
`= 4x^2 + 5/4xyz - 2/3xy^2z - 5x^2yz`
Ta có:
`|y| = 2`
`=> y = +-2`
Thay `x = -1; y = 2` và `z = 1/2` vào C
`4*(-1)^2 + 5/4*(-1)*2*1/2 - 2/3*(-1)*2^2*1/2 - 5*(-1)^2*2*1/2`
`= 4 - 5/4 + 4/3 - 5`
`= -11/12`
Vậy, với `x = -1; y = 2; z = 1/2` thì `B = -11/12`
Thay `x = -1; y = -2; z = 1/2`
`B = 4*(-1)^2 + 5/4*(-1)*(-2)*1/2 - 2/3*(-1)*(-2)^2*1/2 - 5*(-1)^2*(-2)*1/2`
`= 4 + 5/4 + 4/3 + 5`
`= 139/12`
Vậy, với `x = -1; y = -2; z = 1/2` thì `B = 139/12.`

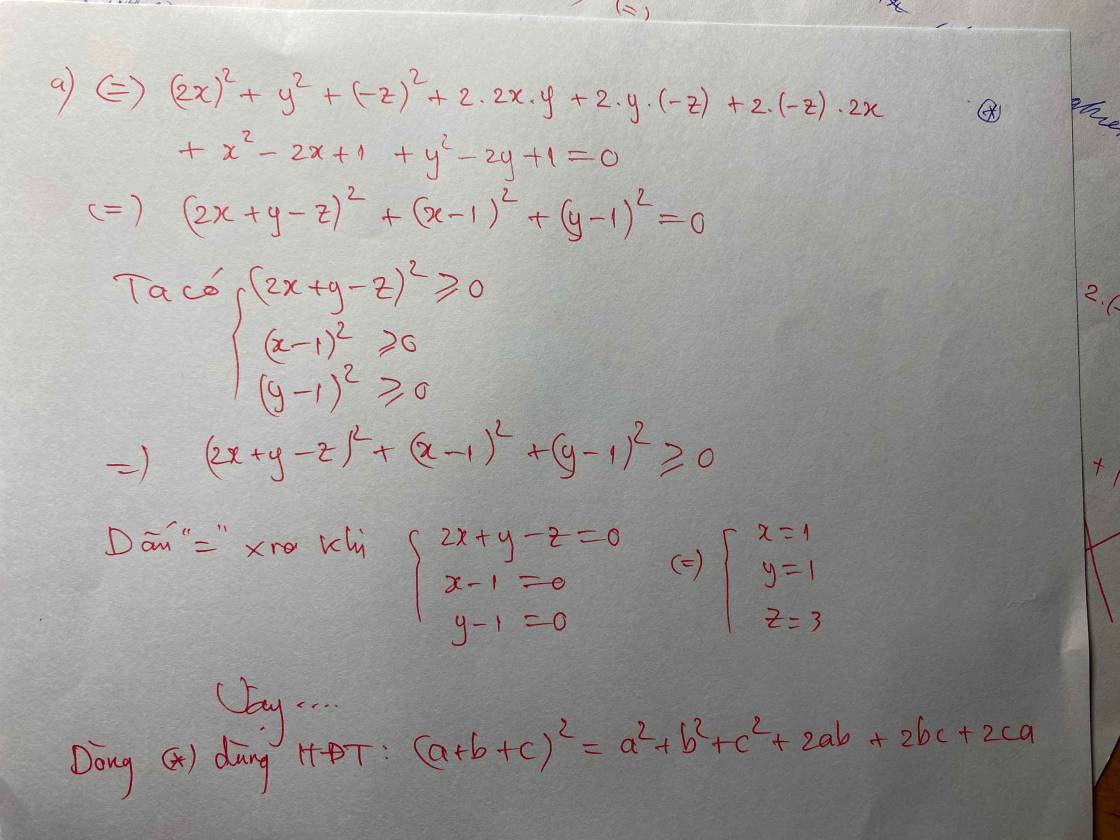
Học tốt nha bn ! ( dòng * ko cần ghi vào đâu bn đây là nháp giở của mik )
Cách 1: Hàng ngang
\(A+B=\left(5x^2y+3xy^2+2yz\right)+\left(-5xy^2+2x^2y-2yz+2\right)\)
\(A+B=5x^2y+3xy^2+2yz-5xy^2+2x^2y-2yz+2\)
\(A+B=\left(5x^2y+2x^2y\right)+\left(3xy^2-5xy^2\right)+\left(2yz-2yz\right)+2\)
\(A+B=7x^2y-2xy^2+2\)
Cách 2: Hàng dọc
\(\begin{matrix}_+A\left(x\right)=5x^2y+3xy^2+2yz\\B\left(x\right)=2x^2y-5xy^2-2yz+2\\\overline{A\left(x\right)+B\left(x\right)=7x^2y-2xy^2+2}\end{matrix}\)
Bạn viết dấu " \(=\) " thẳng hằng với nhau nhá