Cho (P): y=x^2 và đường thẳng (d): y=mx-1 (m là tham số) .Để đường thẳng (d) cắt (P) tại 2 điểm phân biệt thì m nhận giá trị là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 5 2023
a: PTHĐGĐ là:
x^2-4x+4m^2+1=0
Δ=(-4)^2-4(4m^2+1)
=16-16m^2-4=-16m^2+12
Để (d) cắt (P) tại hai điểm phân biệt thì -16m^2+12>0
=>-16m^2>-12
=>m^2<3/4
=>\(-\dfrac{\sqrt{3}}{2}< m< \dfrac{\sqrt{3}}{2}\)
b: x1,x2 nguyên
=>x1+x2 nguyên và x2*x1 nguyên
=>4 nguyên và 4m^2+1 nguyên
=>4m^2 nguyên
=>m^2 nguyên
=>\(m=k^2\left(k\in Z\right)\)
3 tháng 6 2017
- xét phương trình hoành độ giao điểm : \(x^2=\left(2m-1\right)x-m+2\)\(\Leftrightarrow x^2-\left(2m-1\right)x+m-2=0\)có \(\Delta=\left(2m-1\right)^2-4\left(m-2\right)=4m^2-8m+9=\left(2m-1\right)^2+8\ge8\)vậy nên phương trinh luôn có 2 nghiệm phân biệt tức hai đồ thị luôn cắt nhau tại 2 điểm phân biệt A và B
- Có viet : \(\hept{\begin{cases}x_1+x_2=2m-1\\x_1x_2=m-2\end{cases}}\)ta có : \(A\left(x_1,y_1\right)=A\left(x_1,x_1^2\right)\)và \(B\left(x_2,y_2\right)=B\left(x_2,x_2^2\right)\)
nên ta có : \(x_1y_1+x_2y_2=0\Leftrightarrow x_1^3+x_2^3=0\)\(\Leftrightarrow\left(x_1+x_2\right)\left(\left(x_1+x_2\right)^2-3x_1x_2\right)=0\)\(\Leftrightarrow\left(2m-1\right)\left[\left(2m-1\right)^2-3m+6\right]=0\)
- \(2m-1=0\Leftrightarrow m=\frac{1}{2}\)
- \(\left(2m-1\right)^2-3m+6=0\Leftrightarrow4m^2-7m-7=0\)VN
28 tháng 2 2019
2. Cho parabol (P): y = x2 và đường thẳng (d): y = 2(m – 1)x + m2 + 2m (m là tham số, m ∈ R )
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B?
b) Gọi H và K lần lượt là hình chiếu của A và B trên trục hoành.
Tìm m sao cho: OH2 + OK2 = 6 mọi người hướng dẫ mk ý b vs
16 tháng 6 2023
PTHĐGĐ là;
x^2-6x+m-3=0
Δ=(-6)^2-4(m-3)=36-4m+12=-4m+48
Để PT có hai nghiệm phân biệt thì -4m+48>0
=>m<12
(x1-1)(x2^2-x2(x1+x2-1)+x1x2-1)=2
=>(x1-1)(-x1x2+x2+x1x2-1)=2
=>x1x2-(x1+x2)+1=2
=>m-3-6+1=2
=>m-8=2
=>m=10
CM
1 tháng 9 2017
Parabol (P) có đỉnh O nên có dạng y = a x 2 ( a ≠ 0 )
Mà (P) đi qua điểm A (2; 4) nên tọa độ A thỏa mãn phương trình parabol (P) suy ra: 4 = a. 2 2 = 4a ↔ a = 1 (thỏa mãn a ≠ 0)
Phương trình parabol (P) là y = x 2 . (d) cắt (P) tại hai điểm phân biệt thì phương trình hoành độ giao điểm phải có hai nghiệm phân biệt.
Suy ra phương trình x 2 − 2(m – 1)x + 2m + 2 = 0 có hai nghiệm phân biệt
↔ ∆ ’ = [ − ( m – 1 ) ] 2 + 2 m + 2 > 0
↔ m 2 – 2m + 1 + 2m + 2 > 0 ↔ m 2 + 3 > 0 (luôn đúng)
Vậy (d) luôn cắt (P) tại hai điểm phân biệt
Đáp án: D
27 tháng 2 2022
a: Phương trình hoành độ giao điểm là: \(x^2-mx+m-1=0\)
\(\Delta=\left(-m\right)^2-4\cdot\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\)
Để (P) cắt (d) tại hai điểm phân biệt thì m-2<>0
hay m<>2
b: \(\left|x_A-x_B\right|< 3\)
\(\Leftrightarrow\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}< 3\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2< 9\)
\(\Leftrightarrow m^2-4\left(m-1\right)< 9\)
\(\Leftrightarrow\left(m-2\right)^2-3< 0\)
=>(m+1)(m-5)<0
=>-1<m<5
CM
30 tháng 5 2019
Đáp án B
+ Tọa độ giao điểm của hai đường thẳng d và d’ là nghiệm của hệ phương trình:
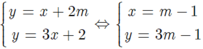
suy ra d và d’ cắt nhau tại M( m-1; 3m-1)
+ Vì ba đường thẳng d; d’ ; d’’ đồng quy nên d’’ qua M ta có
3m-1= -m( m-1) + 2 hay m2+ 2m-3=0
Suy ra m=1 hoặc m= -3
Với m= 1 ta có ba đường thẳng là d: y= x+ 2; d’ : y= 3x+ 2 và d’’: y= -x+ 2 phân biệt và đồng quy tại M(0; 2).
Với m= -3 ta có d và d’’ trùng nhau suy ra m= -3 không thỏa mãn
Vậy m= 1 là giá trị cần tìm.
Chọn B.
Phương trình hoành độ giao điểm là:
\(x^2-mx+1=0\)
\(\text{Δ}=m^2-4\)
Để (P) cắt (d) tại hai điểm phân biệt thì (m-2)(m+2)>0
=>m>2 hoặc m<-2