1.Cho phương trình bậc hai x2_6x+m=0 với m là tham số. Với giá trị nào của m để phương trình có hai nghiệm x1 x2 thỏa mãn (x1)3 + (x2)3 =72
2. Một tổ học sinh chuyển 105 bó sách về thư viện. Đến buổi lao động có 2 học sinh bị ốm không tham gia được, vì vậy mỗi người phải chuyển thêm 6 bó nữa mới hết số sách trên. Hỏi số học sinh trong tổ là bao nhiêu


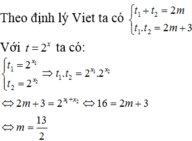

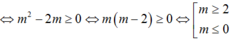
\(\Delta=\left(-6\right)^2-4m=36-4m\)
Để pt có 2 nghiệm phân biệt thì \(36-4m>0\)
\(\Leftrightarrow m< 9\)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=6\\x_1.x_2=m\end{matrix}\right.\)
\(\left(x_1\right)^3+\left(x_2\right)^3=72\)
\(\Leftrightarrow\left(x_1+x_2\right)\left(x_1^2-x_1.x_2+x_2^2\right)=72\)
\(\Leftrightarrow\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-3x_1.x_2\right]=72\)
\(\Leftrightarrow6\left(6^2-3m\right)=72\)
\(\Leftrightarrow36-3m=12\)
\(\Leftrightarrow-3m=-24\)
\(\Leftrightarrow m=8\left(tm\right)\)