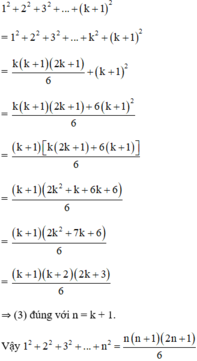BT: Dựa vào các hàng đẳng thức để tính nhanh:
n2 - (n-1)2 + ... + 22 - 12 n là số tự nhiên chẵn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 6 2019
Ta có:
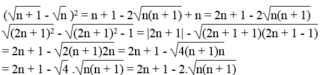
Vế trái bằng vế phải nên đẳng thức được chứng minh.
* Với n = 1, ta có: 2 - 1 2 = 9 - 8
* Với n = 2, ta có: 3 - 2 2 = 25 - 24
* Với n = 3, ta có: 4 - 3 2 = 49 - 48
* Với n = 4, ta có: 5 - 4 2 = 81 - 80
11 tháng 5 2021
Bài 1:
uses crt;
var n,t1,t2,t3,i:integer;
begin
clrscr;
write('Nhap n='); readln(n);
t1:=0;
t2:=0;
for i:=1 to n-1 do
begin
if i mod 2=1 then t1:=t1+i
else t2:=t2+i;
end;
writeln('Tong cac so le nho hon ',n,' la: ',t1);
writeln('Tong cac so chan nho hon ',n,' la: ',t2);
t3:=0;
for i:=1 to 2*n do
t3:=t3+i;
writeln('Tong cac so trong day so tu 1 toi 2*',n,' la: ',t3);
readln;
end.
11 tháng 2 2021
a) uses crt;
var n,x,i:longint;
lt:real;
begin
clrscr;
write('Nhap co so n=');readln(n);
write('Nhap so mu x='); readln(x);
lt:=1;
for i:=1 to x do
lt:=lt*n;
writeln(n,'^',x,'=',lt:0:0);
readln;
end.
13 tháng 4 2022
uses crt;
var i,n,s:integer;
begin
clrscr;
readln(n);
s:=0;
i:=0;
while i<=n do
begin
i:=i+1;
s:=s+i*i;
end;
writeln(s);
readln;
end.
ML
19 tháng 3 2023
Câu 1:
Program HOC24;
var i,p: integer;
t: longint;
begin
write('Nhap P: '); readln(p);
t:=0;
for i:=1 to p do if i mod 2<>0 then t:=t+i;
write('Tong cac so le la: ',t);
readln
end.
HT
3
18 tháng 11 2015
n2 + 3 chia hết cho n + 2
n + 2 chia hết cho n + 2
=> n(n + 2) chia hết cho n + 2
n2 + 2n chia hết cho n + 2
=> (n2 + 2n - n2 + 3) chia hết cho n + 2
2n - 3 chia hết cho n + 2
n + 2 chia hết cho n + 2
=> 2(n + 2) chia hết cho n + 2
2n + 4 chia hết cho n + 2
=>(2n + 4 - 2n + 3) chia hết cho n + 2
7 chia hết cho n + 2
n + 2 thuộc U(7) = {-7;-1;1;7}
n + 2 = -7 => n = -9
n + 2 = -1 => n = -3
n + 2 = 1 => n = -1
n + 2 = 7 => n = 5
Mà n là số tự nhiên nên n = 5
18 tháng 11 2015
n^2+3 chia hết cho n+2
=>(n^2+4n+4)-4n-1 chia hết cho n+2
=>(n+2)^2 -(4n+1) chia hết cho n+2
=>4n+1 chia hết cho n+2(vì (n+2)^2 chia hết cho n+2)
=>4(n+2)-7chia hết cho n+2
=>7 chia hết cho n+2
=>n+2 thuộc Ư(7)
=>n+2=(1,7)
=> n=-1;5 mà n là số tự nhiên nên n=5
đáp số n=5
TM
0
CM
21 tháng 6 2018
+ Với n = 1 :
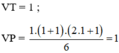
⇒ (3) đúng với n = 1
+ Giả sử đẳng thức (3) đúng với n = k nghĩa là :
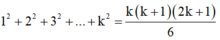
Cần chứng minh (3) đúng khi n = k + 1, tức là:
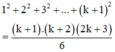
Thật vậy:
