Một bệnh viện đặt một cơ sở sản xuất 600 giường bệnh. Cơ sở sản xuất dự định sản xuất trong một số tháng và mỗi tháng làm một lượng sản phẩm như nhau. Tuy nhiên khi tiến hành cơ sở đã sản xuất mỗi tháng thêm 100 sản phẩm so với dự định nên đã hoàn thành công việc sớm hơn 1 tháng. Hỏi cơ sở sản xuất lúc đầu dự định sản xuất trong bao lâu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sau 5 tháng sản xuất được:
9828:4*5=12285 sp
Còn lại:
12285*2/3=8190sp

Đổi: \(1\)tháng = \(30\)ngày.
Số ngày trong \(9\)tháng là:
\(30\times9=270\)(ngày)
Trong \(9\)tháng cơ sở đó sản xuất được số sản phẩm là:
\(412\times270=111240\)(sản phẩm)

Sau tháng cuối năm sản xuất được:
14386 + 495 = 14881 (quyển vở)
Cả năm cơ sở đó sản xuất được:
14881 + 14386 = 29267 (quyển vở)
Sáu tháng cuối năm cơ sở đó sản xuất đc số vở là:
14 386+ 495=14881(quyển vở)
Cả năm đó cơ sở đã sản xuất đc số vở là:
14881+14386=29267(quyển vở)
Đ/S: 29269 quyển vở

Sáu tháng cuối năm cơ sở đó sản xuất đc số vở là:
14386+ 495 = 14881 (quyển vở)
Cả năm đó cơ sở đã sản xuất đc số vở là:
14881 + 14386 = 29267 (quyển vở)
Đ/S: 29269 quyển vở

sáu tháng cuối sản xuất đc
14 386 + 495 = 14 881 quyển
cả năm sản xuất đc
14 386 + 14 881 = 29 267 quyển
đáp số : 29 267 quyển

Đáp án C
Gọi số chiếc nón lá mỗi ngày cơ sở đó làm được là x (chiếc)
Số ngày cơ sở đó dự kiến làm hết 300 chiếc nón lá là: 300/x (ngày)
Sau khi làm tăng thêm 5 chiếc nón lá một ngày thì thời gian cơ sở đó làm hết 300 chiếc nón lá là: 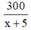 (ngày).
(ngày).
Theo đề bài ta có phương trình:
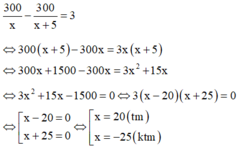
Vậy theo dự kiến, mỗi ngày cơ sở đó làm được 20 chiếc nón lá.
Gọi thời gian dự định sản suất là x (tháng) với x>1
Mỗi tháng cơ sở dự định sản xuất được: \(\dfrac{600}{x}\) giường bệnh
Thời gian sản xuất thực tế: \(x-1\) tháng
Mỗi tháng thực tế sản xuất được: \(\dfrac{600}{x-1}\) giường bệnh
Do mỗi tháng sản xuất thêm 100 sp so với dự định nên ta có pt:
\(\dfrac{600}{x-1}-\dfrac{600}{x}=100\)
\(\Rightarrow6x-6\left(x-1\right)=x\left(x-1\right)\)
\(\Leftrightarrow x^2-x-6=0\Rightarrow\left[{}\begin{matrix}x=3\\x=-2\left(loại\right)\end{matrix}\right.\)