cho tam giác ABC có góc B = 60 độ,góc C= 40 độ
AD là tia phân giác của góc BAC
kẻ AH vuông góc BC
a,tính góc BAC
b,tính góc ADH
c,tính góc HAD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 11 2023
a: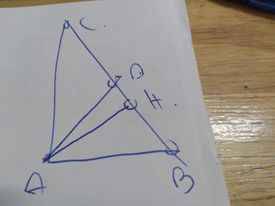 
b: AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{1}{2}\cdot\widehat{BAC}=\dfrac{1}{2}\cdot90^0=45^0\)
Xét ΔADC có \(\widehat{ADH}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADH}=\widehat{DAC}+\widehat{DCA}\)
=>\(\widehat{ADH}=45^0+30^0=75^0\)
b: ΔHAD vuông tại H
=>\(\widehat{HAD}+\widehat{HDA}=90^0\)
=>\(\widehat{HAD}+75^0=90^0\)
=>\(\widehat{HAD}=15^0\)
Vì \(\widehat{DAH}< \widehat{DAB}\)
nên AH nằm giữa AD và AB
=>\(\widehat{DAH}+\widehat{BAH}=\widehat{BAD}\)
=>\(\widehat{BAH}+15^0=45^0\)
=>\(\widehat{BAH}=30^0>\widehat{HAD}\)
d: \(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
\(\widehat{HAC}+\widehat{C}=90^0\)(ΔAHC vuông tại H)
Do đó: \(\widehat{ABC}=\widehat{HAC}\)
26 tháng 11 2023
`a)`
`b)`
Có `Delta ABC` vuông tại `A` có `hat(C)=30^0`
`=>hat(B)=60^0`
`AD` là phân giác `hat(BAC)=>hat(BAD)=hat(A_3)=1/2hat(BAC)`
`=>hat(BAD)=hat(A_3)=1/2*90^0=45^0`
`Delta BAD` có `hat(B)+hat(D_1)+hat(BAD)=180^0`
hay `60^0+hat(D_1)+45^0=180^0`
`=>hat(D_1)=180^0-60^0-45^0=75^0`
`c)`
Có `Delta AHD` vuông tại `H(AH⊥BC)` có `hat(D_1)=75^0`
`=>hat(A_1)=15^0`
Có `hat(A_1)+hat(A_2)=hat(BAD)`
hay`15^0+hat(A_2)=45^0`
`=>hat(A_2)=30^0`
Có `15^0<30^0`
`=>hat(A_1)<hat(A_2)`
`d)`
Có `hat(A_1)+hat(A_3)=hat(HAC)`
hay `15^0+45^0=hat(HAC)`
`=>hat(HAC)=60^0`
Có `60^0=60^0`
`=>hat(B)=hat(HAC)`
30 tháng 10 2017
a, Ta có:
Góc A + góc B + góc C = 180o
=> Góc C = 180o - ( góc A + góc B)
=> Góc C = 180o - ( 90o + 60o)
=> Góc C = 30o
b, Vì AD là tia phân giác góc A
Mà góc A = 90o (giả thiết)
=> Góc BAD = DAC = 90o : 2 = 45o
Ta có: Góc BAD + góc ABD + góc ADB = 180o
=> 45o + 60o + góc ADB = 180o
=> góc ADB = 75o
c, Ta có: góc AHD + góc HDA + góc DAH = 180o
=> góc DAH = 180o - 90o - 75o
=> góc DAH = 15o
TT
1 tháng 11 2017
Vì góc A = 90o , AD là tia phân giác góc A nên góc BAD = góc DAC = 90/2 = 45o.
Vì AH vuông góc với BC nên góc AHC=900
Trong tam giác HAC có : (góc) HAC + HCA + AHC = 180o
===> góc HAC + 400+900 = 1800
===> góc HAC = 500
Vì góc HAC > góc DAC (900>450) nên tia AD nằm giữa hai tia AC và AH
===> góc HAD + góc DAC = góc HAC
====> góc HAD + 450=500
===> góc HAD = 50
16 tháng 9 2016
Ta có hình vẽ:
Kẻ đường thẳng aa' đi qua điểm A sao cho aa' // BC
Vì AD là tia phân giác của CAB
=> \(CAD=DAB=\frac{CAB}{2}=\frac{90^o}{2}=45^o\)
Ta có: ACB = CAa' = 40o (so le trong)
Mà CAa' + CAD = DAa'
=> 40o + 45o = DAa'
=> DAa' = 85o
Do AH vuông góc với BC; aa' // BC => AH vuông góc với aa'
=> HAa' = 90o
Lại có: DAa' + HAD = HAa'
=> 85o + HAD = 90o
=> HAD = 90o - 85o
=> HAD = 5o
Bạn tự vẽ hình nha
a) trong tam giac ABC có: ABC + BAC + ACB =180 độ ( là góc ABC,ACB,BAC )
Mà góc ABC = 60 độ, góc ACB = 40 độ => góc BAC = 80 độ
b) AD là tia p/g góc BAC => góc BAD = góc DAC = 1/2 góc BAC = 40 độ
trong tam giác ABD có : góc ABD = 60 độ , góc BAD = 40 độ
=> góc ADB = 80 độ hay góc ADH = 80 độ ( vì H nằm trên BD )
c) tự lam nha bạn , giống mấy câu trên thôi ( -....- )