Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABD vuông tại A và ΔHAD vuông tại H có
góc ADH chung
Do đó: ΔABD\(\sim\)ΔHAD
b: \(BD=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(HD=\dfrac{AD^2}{BD}=1.8\left(cm\right)\)
a, Xét tam giác AHB và tam giác BCD, có:
AHB = BCD = 90o
B1 = B2
=> Tam giác AHB ~ tam giác BCD (g_g)
b, Theo ý a, ta có:
Tam giác AHB ~ tam giác BCD => AH/BC = AB/BD
=> AH = AB.BC/BD = 12.9/15 = 7,2 cm
=> AH = 7,2 cm
c, Vì BD là đường chéo hình chữ nhật ABCD nên B1 = B2 = D1 = D2
Xét tam giác AHB và tam giác DHA, có
AHB = DHA = 90o
D1 = B1 (cmt)
=> Tam giác AHB ~ tam giác DHA (g_g)
=> AH/BH = DH/AH (dpcm)
a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc HBA chung
Do đó: ΔABD\(\sim\)ΔHBA
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(HB=\dfrac{AB^2}{BD}=6.4\left(cm\right)\)
a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc HBA chung
Do đó: ΔABD\(\sim\)ΔHBA
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(HB=\dfrac{AB^2}{BD}=6.4\left(cm\right)\)
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
góc ABH=góc BDC
=>ΔAHB đồng dạng với ΔBCD
b: BD=căn 9^2+12^2=15cm
AH=9*12/15=108/15=7,2cm
c: Xét ΔHAD có HN/HA=HP/HD
nên NP//AD và NP=AD/2
=>NP//BC và NP=BC/2
=>NP//BM và NP=BM
=>BNPM là hình bình hành
a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc ABD chung
=>ΔABD đồng dạng với ΔHBA
b: BD=căn 3^2+4^2=5cm
HB=AB^2/BD=3,2cm
c: AD là phân giác
=>ED/EB=AD/AB
mà AD/AB=AH/BH
nên ED/EB=AH/BH
a: Xét ΔHAD vuông tại H và ΔABD vuông tại A có
góc HDA chung
=>ΔHAD đồng dạng với ΔABD
b: ΔABD vuông tại A có AH là đường cao
nên DA^2=DH*DB
c: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
AH=6*8/10=4,8cm
DH=6^2/10=3,6cm
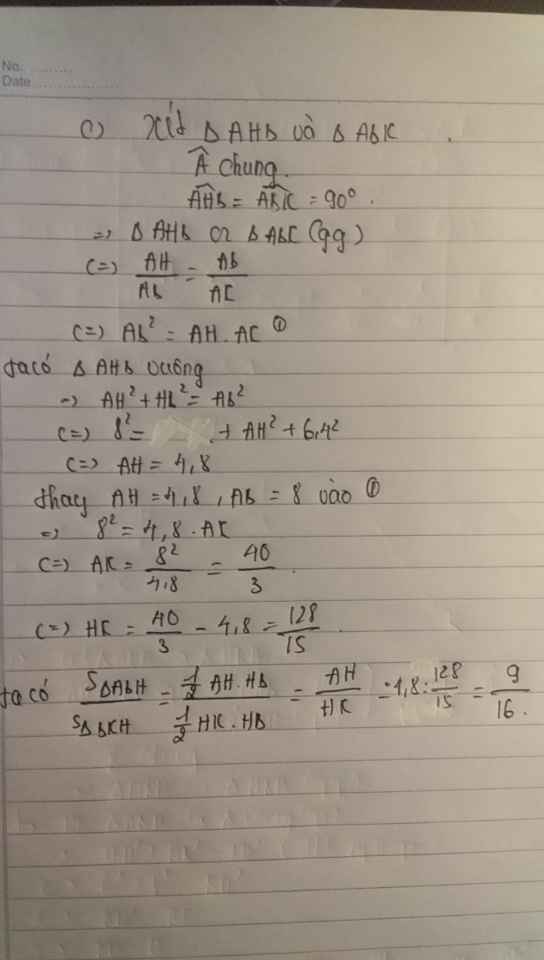
a) Xét ΔABD vàΔ HAD có:
\(\widehat{DAB}\) =\(\widehat{AHB}\)= 90o( gt)
\(\widehat{D}\) chung
⇒Δ ABD ∼ ΔHAD(g-g)
b) Áp dụng định lí Py-ta-go vào Δ ABD vuông tại A ta có:
BD=\(\sqrt{AD^2+AB^2}\)=\(\sqrt{3^2+4^2}\)=\(\sqrt{25}\)=5(cm)
Theo câu a ta có:Δ ABD ∼ ΔHAD
⇒\(\dfrac{BD}{AD}\)=\(\dfrac{AD}{HD}\)hay \(\dfrac{5}{3}\)=\(\dfrac{3}{HD}\)⇒HD=\(\dfrac{3.3}{5}\)=1,8 (cm)