Chứng minh rằng :tam giác có 2 đường phân giác bằng nhau là tam giác cân.
giải giúp tôi với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn kẻ tam giác ABC có phân giác BD và CE bằng nhau; dựng hình bình hành EBDH
Giả sử tam giác ko cân
TH1: Góc B > C => góc DBC > BCE và góc ABD > ACE
Xét tam giác BCD và CBE có:
BD = CE (gt)
BC chung
góc DBC > BCE
==> CD > BE (1)
Vì EBDH là HBH => BE = DH (2) và EH = BD => EH = CE (3)
Từ (1)(2) => CD > HD => góc CHD > DCH (☺)
Lại có: góc DHE = DBE > ACE (☻)
Từ (☺)(☻) => CHD + DHE > DCH + ACE <=> góc EHC > ECH => CE > HE mâu thuẫn với (3)
TH2: Góc B < C. CM tương tự => mâu thuẫn
Vậy góc B = C => tam giác cân => (đpcm)

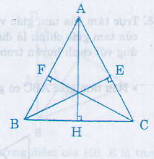
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=>
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
BD=CE
góc ABD=góc ACE
=>ΔADB=ΔAEC
=>AB=AC
=>ΔABC cân tại A
b: ΔABC cân tại A
mà AD là đường phân giác
nên AD vuông góc BC
Xét ΔABC có
AD,CH là đường cao
AD cắt CH tại D
=>D là trực tâm
=>BD vuông góc AC
