giúp em với huhu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 1:
\(\left(4x+3\right)\left(3x^2+x-2\right)\left(2x^2-3x-5\right)=0\\ \Leftrightarrow\left(4x+3\right)\left(3x-2\right)\left(x+1\right)\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=-1\\x=\dfrac{2}{3}\\x=\dfrac{5}{2}\end{matrix}\right.\\ \Leftrightarrow A=\left\{-1;-\dfrac{3}{4};\dfrac{2}{3};\dfrac{5}{2}\right\}\)
Câu 2:
\(\left(x^2-4\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=3\end{matrix}\right.\Leftrightarrow A=\left\{-2;2;3\right\}\\ \left|5x\right|-11\le0\Leftrightarrow\left|5x\right|\le11\Leftrightarrow-11\le5x\le11\\ \Leftrightarrow-\dfrac{11}{5}\le x\le\dfrac{11}{5}\\ \Leftrightarrow B=\left[-\dfrac{11}{5};\dfrac{11}{5}\right]\)
\(\Leftrightarrow A\cap B=\left\{-2;2\right\}\\ A\cup B=\left[-\dfrac{11}{5};3\right]\\ A\B=\left\{3\right\}\)

a, Vì SA ; SB lần lượt là tiếp tuyến (O) với A;B là tiếp điểm
nên ^SAO = ^SBO = 900
Xét tứ giác SAOB ta có
^SAO + ^SBO = 1800
mà 2 góc này đối
Vậy tứ giác SAOB là tứ giác nt 1 đường tròn
b, Vì H là trung điểm CD => OH vuông CD
Xét tứ giác AHOS có
^OHS = ^OAS = 900
mà 2 góc này kề, cùng nhìn cạnh OS
Vậy tứ giác AHOS là tứ giác nt 1 đường tròn
=> ^OAH = ^OSH ( góc nt chắn cung HO )
c, Xét tam giác SAC và tam giác SDA ta có
^S _ chung
^SAC = ^SDA (cùng chắn cung AC )
Vậy tam giác SAC ~ tam giác SDA (g.g)
\(\dfrac{SA}{SD}=\dfrac{SC}{SA}\Rightarrow SA^2=SC.SD\)(1)
Ta có ^SAB = ^SBA do SA = SB ( tiếp tuyến cắ nhau )
mà ^AHS = ^AOS ( góc nt chắn cung AS của tứ giác ASOH )
Mặt khác ^AOS = ^SBA ( góc nt chắn cung AS của tứ giác ASBO )
=> ^SAE = ^SHA
Xét tam giác SAE và tam giác SHA ta có
^S _ chung
^SAE = ^SHA (cmt)
Vật tam giác SAE ~ tam giác SHA (g.g)
\(\dfrac{SA}{SH}=\dfrac{SE}{SA}\Rightarrow SA^2=SE.SH\)(2)
Từ (1) ; (2) suy ra \(SE.SH=SC.SD\)

1 \(=\dfrac{4x^2+7+5x^2-7}{3x^2y}=\dfrac{9x^2}{3x^2y}=\dfrac{3}{y}\)
2: \(=\dfrac{6x+3x+27}{x+3}=\dfrac{9x+27}{x+3}=9\)
3: \(=\dfrac{x^2-10x+25}{x-5}=\dfrac{\left(x-5\right)^2}{x-5}=x-5\)
4: \(=\dfrac{x+y}{xy\left(x+y\right)}=\dfrac{1}{xy}\)
5: \(=\dfrac{2x-6+3x+9+1}{\left(x-3\right)\left(x+3\right)}=\dfrac{5x+4}{\left(x-3\right)\left(x+3\right)}\)



a: Thay x=-2 vào (1), ta được:
4+8+2m-1=0
=>2m+11=0
hay m=-11/2
b: \(\text{Δ}=\left(-4\right)^2-4\left(2m-1\right)\)
=16-8m+4
=-8m+20
Để phương trình có hai nghiệm phân biệt thì -8m+20>0
=>-8m>-20
hay m<5/2
Theo đề, ta có: \(x_1^2+x_2^2+x_1x_2=m^2-2m\)
\(\Leftrightarrow m^2-2m=\left(x_1+x_2\right)^2-x_1x_2\)
\(\Leftrightarrow m^2-2m=\left(-4\right)^2-\left(2m-1\right)\)
\(\Leftrightarrow m^2-2m=16-2m+1=17\)
hay \(m=-\sqrt{17}\)









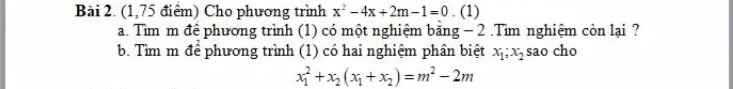
bài trên hay dưới v bn?
dạ trên ạ