Cho hình bình hành ABCD. Trên AB lấy M, trên CD lấy N sao cho AM = CN. Gọi O là giao điểm 2 đường chéo của ABCD. CM O là trung điểm của MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 11 2023
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b:ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN
KV
11 tháng 10 2023
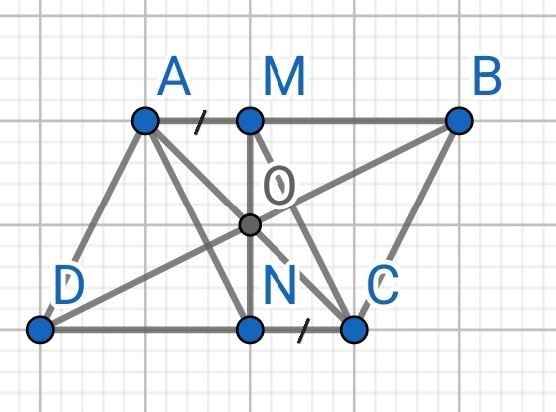a) Do ABCD là hình bình hành
AB // CD
⇒ AM // CN
Tứ giác AMCN có:
AM // CN (cmt)
AM = CN (gt)
⇒ AMCN là hình bình hành
⇒ AN // CM
b) Do ABCD là hình bình hành
O là giao điểm của AC và BD
⇒ O là trung điểm của AC
Lại có AMCN là hình bình hành
O là trung điểm của AC (cmt)
⇒ O là trung điểm của MN
CM
22 tháng 9 2019
Chọn D
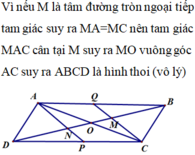
Vì nếu M là tâm đường tròn ngoại tiếp tam giác suy ra MA = MC nên tam giác MAC cân tại M suy ra MO vuông góc AC suy ra ABCD là hình thoi (vô lý)
Hình bình hành ABCD . Trên cạnh AB và CD lấy M và N sao cho AM và CN .
9 tháng 11 2021
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
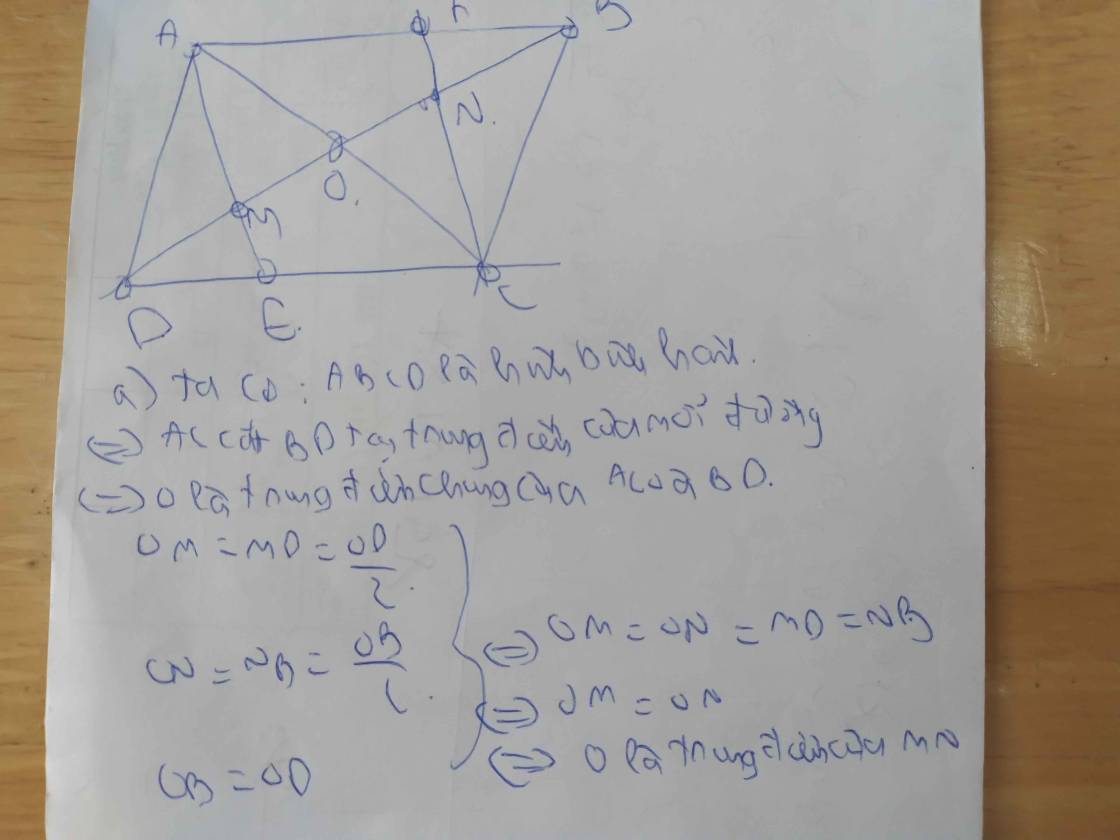
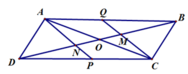
Ta có : AB//CD ( ABCD là HBH )
=> AM//CN và AM=CN (gt)
=> AMCN là HBH
Ta lại có : AC cắt BD tại O
Hay O là trung điểm của AC và DB
Mà : AMCN là HBH
=> O cũng là trung điểm của MN và M,O,N thẳng hàng .