cho tam giác abc điểm o nằm trong tam giác. vẽ các điểm D,E,F sao cho O là trung điểm của các đoạn thẳng AD, BE , CF. CMR tam giác ABC = tam giác DEF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
9 tháng 2 2020
i nhanh nhất mình khuyên họ hàng anh chị em mình k cho làm ơn 2 giờ mình cần gấp
24 tháng 3 2023
Xét ΔBDE và ΔAFD có
BE=AD
góc EBD=góc DAF
AF=BD
=>ΔBDE=ΔAFD
=>DE=FD
Xét ΔBDE và ΔCEF có
BE=CF
góc DBE=góc ECF
BD=CE
=>ΔBDE=ΔCEF
=>DE=EF=FD
=>ΔDEF đều
14 tháng 3 2015
Tam giác ABC đều
=> Góc A=Góc B=Góc C
Chứng minh Tam giác ADE và Tam giác BED:
AD=BE
Góc A=Góc B
AF=BD
=> Tam giác ADE=Tam giác EBD(c.g.c) (1)
=>DF=ED (3)
Tương tự chứng minh Tam giác ECF=Tam giác FAD(c.g.c) (2)
EF=DF (4)
Từ (1) và (2) =>Tam giác BED=Tam giác CFE
=>ED=FE (5)
Từ (3);(4);(5) => DF=DE=FE
=> Tam giác DEF là tam giác đều
9 tháng 9 2017
\(\frac{OA}{AD}=\frac{S_{AOB}}{S_{ABD}}=\frac{S_{AOC}}{S_{ACD}}=\frac{S_{AOB}+S_{AOC}}{SABC}\)
Tương tự rồi cộng lại ta đc
\(\frac{OA}{AD}+\frac{OB}{BE}+\frac{OC}{CF}=\frac{2\left(S_{AOB}+S_{BOC}+S_{COA}\right)}{S_{ABC}}=2\)
B
8 tháng 9 2017
Bài Giải
Đặt SBOC=x2,SAOC=y2,SAOB=z2 ⇒SABC=SBOC+SAOC+SAOB=x2+y2+z2
Ta có : ADOD =SABCSBOC =AO+ODOD =1+AOOD =x2+y2+z2x2 =1+y2+z2x2
⇒AOOD =y2+z2x2 ⇒√AOOD =√y2+z2x2 =√y2+z2x
Tương tự ta có √OBOE =√x2+z2y2 =√x2+z2y ;√OCOF =√x2+y2z2 =√x2+y2z
⇒P=√x2+y2z +√y2+z2x +√x2+z2y ≥x+y√2z +y+z√2x +x+z√2y
=1√2 [(xy +yx )+(yz +zy )+(xz +zx )]≥1√2 (2+2+2)=3√2
Dấu "=" xảy ra khi x=y=z⇒SBOC=SAOC=SAOB=13 SABC
⇒ODOA =OEOB =OFOC =13 ⇒O là trọng tâm của tam giác ABC
Vậy MinP=3√2 khi O là trọng tâm của tam giác ABC
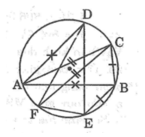
+ O trung điểm AD => AO = OD
+ O trung điểm BE => BO = BE
+ O trung điểm CF => OC = OF
+ Xét ∆FOE và ∆COB có:
OF = OC (cmt)
góc FOE = góc BOC (đđ) => ∆FOE = ∆COB (c-g-c) => FE = BC (2 cạnh tương ứng)
OE = OB (cmt)
Chứng minh tương tự với ∆FOD và ∆COA với ∆BOA và ∆EOD
=> có AB = ED và AC = FD
+ Xét ∆ ABC và ∆ DEF có:
FE = BC (cmt)
AB = ED (cmt) => ∆ ABC = ∆ DEF (c-c-c) (đpcm)
AC = FD (cmt)