Cho Parabol (P) y= ax^2
a) Tìm a biết rằng (P) đi qua điểm K (2;4) vẽ đồ thị (P) với a vừa tìm được
b) Với a tìm được ở câu a, hãy xác định để đường thẳng (d) tại 2 điểm phân biệt A( x1, y1), B(x2, y2) sao cho y1 - y2= 42
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do (P) qua A;B;C, thay tọa độ A, B, C vào pt (P) ta được:
\(\left\{{}\begin{matrix}a+b+c=-1\\4a+2b+c=3\\a-b+c=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=1\\c=-3\end{matrix}\right.\)
\(\Rightarrow\left(P\right):\) \(y=x^2+x-3\)

Gọi parabol có dạng y=ax2
Vì P đi qua A(-2;-2)\(\Rightarrow\)a=-\(\dfrac{1}{2}\)
\(\Rightarrow\)P có dạng y= -\(\dfrac{1}{2}\)x2 (1)
vì khoảng cách đến trục hoành gấp đôi khoảng cách đến trục tung\(\Rightarrow\)\(\left|y\right|\)=2\(\left|x\right|\)
Nếu x>0 thì y>0 (vô lí)
Nếu x<0 thì y<0\(\Rightarrow\)y=-2x (2)
Từ (1) và (2) có x=4 và y=-2
hoặc x=-4 và y= -2
vậy M(4;-2) hoặc(-4;-2)

a) Do parabol qua điểm O nên ta có thể giả sử phương trình của Parabol có dạng : y = ax2 \(\left(a\ne0\right)\)
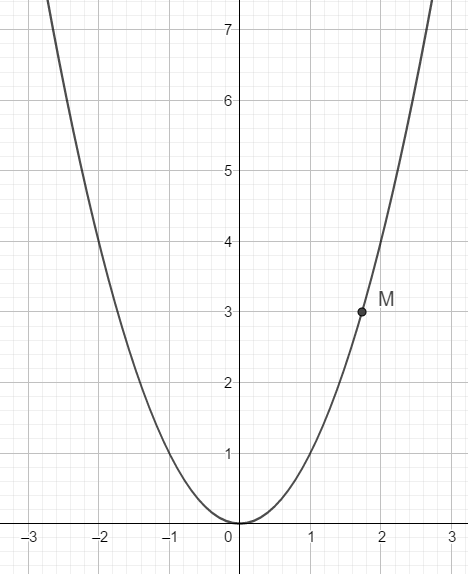
Parabol qua điểm \(M\left(\sqrt{3};3\right)\) nên ta thấy ngay \(3=a\left(\sqrt{3}\right)^3\Rightarrow a=1\)
Vậy phương trình parabol là \(y=x^2\)
Ta có bảng giá trị:
| x | 2 | 1 | 0 | -1 | -2 |
| y | 4 | 1 | 0 | 1 | 4 |
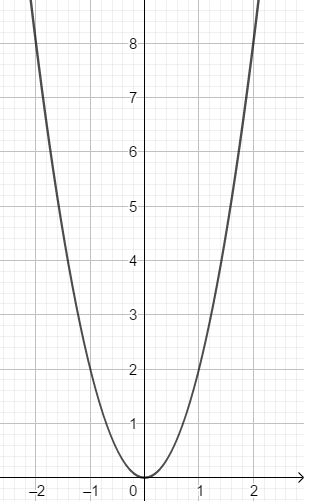
b) Vì \(K\left(\sqrt{2};4\right)\) thuộc parabol (P) nên \(4=a\left(\sqrt{2}\right)^2\Leftrightarrow a=2\)
Vậy phương trình parabol cần tìm là: \(y=2x^2\)
Bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 8 | 2 | 0 | 2 | 8 |

ta có hệ sau :
\(\hept{\begin{cases}a.3^2+b.3-1=-7&-\frac{b}{2a}=1&\end{cases}\Leftrightarrow\hept{\begin{cases}9a+3b=-6\\b=-2a\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-2\\b=4\end{cases}}}\)
vậy \(2a+b=0\)
a: Thay x=2 và y=4 vào (P), ta được:
a*2^2=4
=>a=1