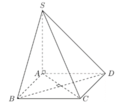
cho S.ABCD có đáy ABCD ;là hình vuông a, SA vuông góc (ABCD), SA = \(a\sqrt{b}\) . tính :
a/ ((SC,(ABCD))
b/ (SB,(SAD))
c/ (SC,(SAB))
d/ (SB,(SAC))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Số mặt bên là 4
\(SAB;SAD;SBC;SCD\)
2: Số cạnh đáy là 4
AB,BC,CD,DA
3: SA và BC là hai đường thẳng chéo nhau
4: 4 đỉnh: A,B,C,D
5: Có 7 mặt: \(SAB;SAD;SBC;SCD;SAC;SBD;ABCD\)
6C


Đáp án D
Ta có: S A = S C . sin 60 ∘ = a 3 2 , A C = S C . c os 60 ∘ = a 2
2 A B 2 = A C 2 = a 2 4 ⇒ S A B C D = A B 2 = a 2 8
Thể tích khối chóp S.ABCD là: V = 1 3 S A . S A B C D = 1 3 . a 3 2 . a 2 8 = a 3 3 48 .

Đáp án A
Tam giác SAC vuông tại A suy ra:
S A = S C 2 − A C 2 = a 5 2 − a 2 2 = a 3
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 . S A . S S . A B C D = 1 3 . a 3 . a 2 = a 3 3 3

Đáp án D
Diện tích hình chữ nhật ABCD là S = 2a2, chiều cao SA =a.
Vậy thể tích khối chóp S.ABCD là V = 1 3 . 2 a 2 . a = 2 3 a 3
Sửa đề; SA=a*căn 2
a: (SC;(ABCD))=(CS;CA)=góc SCA
AC=căn 2*AB^2=a*căn 2
tan SCA=SA/AC=1
=>góc SCA=45 độ
b: BC vuông góc AD
BC vuông góc SA
=>BC vuông góc (SAD)
=>(SB;(SAD))=(SB;SC)
SC=căn SA^2+AC^2=2a
SB=căn SA^2+AB^2=căn 2a^2+a^2=a*căn 3
BS^2+BC^2=SC^2
=>ΔBSC vuông tại B
=>(SB;SC)=góc BSC
sin BSC=BC/SC=1/2
=>góc BSC=30 độ
c: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>(SC;(SAB))=(SC;SB)=góc CSB=30 độ