Viết phương trình tiếp tuyến của ĐTHS \(y=\dfrac{-1}{3}x^3-2x^2-3x+1\)
a) Có hệ số góc lớn nhất
b) Có hệ số góc nhỏ nhất (Tức là y''(\(x_0\))=0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
- Ta có:
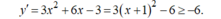
- Hệ số góc của tiếp tuyến đồ thị hàm số y = x 3 + 3 x 2 – 3 x là một giá trị của y’, nên hệ số góc nhỏ nhất là k = -6, ứng với hoành độ tiếp điểm là x = -1 ⇒ y = 5.
→ Phương trình tiếp tuyến là:
y = -6(x + 1) + 5, hay y = -6x - 1.

** Hệ số góc
Lời giải:
Bạn chỉ cần nhớ công thức PTTT:
$y=y'(x_0)(x-x_0+y(x_0)$
Gọi $M(x_0,y_0)$ là tiếp điểm:
$y'=3x^2-3=9\Leftrightarrow x=\pm 2$
Nếu $x_0=2\Rightarrow y_0=4$ thì PT tiếp tuyến tại $(2,4)$ là:
$y=9(x-2)+4=9x-14$
Nếu $x_0=-2\Rightarrow y_0=0$. PT tiếp tuyến tuyến tại $(-2,0)$ là:
$y=9(x+2)+0=9x+18$
Giải thích cho em hiểu rõ hơn Tại sao y 0 lại bằng 4 được không ạ

Đáp án là A.
• Gọi M x 0 ; y 0 ∈ C là toạ độ tiếp điểm.
• Ta có: y ' x 0 = 3 x 0 2 − 6 x 0 = 3 x 0 − 1 2 − 3 ≥ − 3.
Dấu "=" xẩy ra khi và chỉ khi x 0 = 1 .
Tiếp tuyến có hệ số góc nhỏ nhất khi x 0 = 1 ⇒ y 0 = 0
• Phương trình tiếp tuyến cần tìm: y = − 3 x + 3
Lời giải:
a. PTTT của ĐTHS tại điểm $(x_0,y_0)$ là:
$y=y'(x_0)(x-x_0)+y_0$
$=(-x_0^2-4x_0-3)(x-x_0)+y_0$
Hệ số góc max $\Leftrightarrow -x_0^2-4x_0-3$ max
Mà:
$-x_0^2-4x_0-3=1-(x_0+2)^2\leq 1$ nên $-x_0^2-4x_0-3$ max bằng $1$ khi $x_0=-2$
Vậy PTTT cần tìm là:
$y=y'(-2)(x+2)+y(-2)=1(x+2)+\frac{5}{3}=x+\frac{11}{3}$
b.
Hệ số góc nhỏ nhất đâu đồng nghĩa với $y''(x_0)=0$ đâu bạn?)
Để pttt tại $x=x_0$ có hệ số góc min thì nghĩa là $f'(x_0)=-x_0^2-4x_0-3$ min
Mà $f'(x_0)$ không tồn tại min trên $\mathbb{R}$ nên không có pttt thỏa mãn.