Cho góc \(\widehat{xOy}=90^o.\)GỌI Oz là tia phân giác của góc xOy. Lấy M thuộc tia Oz. Gọi A, B lần lượt là hình chiếu của M lên Ox, Oy. Lấy I thuộc AM. Tia tạo với OI một góc bằng \(\widehat{AIO}\)cắt tia MB tại K ( góc AIO = góc OIK). Tính số đo góc\(\widehat{IOK}.\)
A O K B M I
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

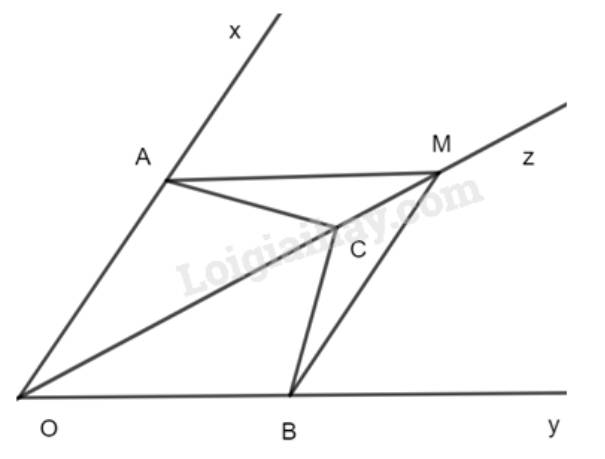
a) Trong \(\Delta OAC\) có: \(\widehat {AOC}+\widehat {OAC}+\widehat {OCA}=180^0\)
Trong \(\Delta OBC\) có: \(\widehat {BOC}+\widehat {OBC}+\widehat {OCB}=180^0\)
Mà \(\widehat {AOC} = \widehat {BOC}\)(do Oz là phân giác góc xOy) và \(\widehat {CAO}=\widehat {CBO}\)
Do đó, \(\widehat {OCA}=\widehat {OCB}\).
Xét \(\Delta OAC\) và \(\Delta OBC\) có:
\(\widehat {AOC} = \widehat {BOC}\) (cmt)
OC chung
\(\widehat {OCA} = \widehat {OCB}(cmt)\)
\(\Rightarrow \Delta OAC = \Delta OBC\)(g.c.g)
b) Do \(\Delta OAC = \Delta OBC\) nên AC=BC ( 2 cạnh tương ứng)
Vì \(\widehat {ACO}\) và \(\widehat {ACM}\) kề bù
\(\widehat {BCO}\) và \(\widehat {BCM}\) kề bù
Mà \(\widehat {ACO} = \widehat {BCO}\) nên \(\widehat {ACM} = \widehat {BCM}\)
Xét \(\Delta MAC\) và \(\Delta MBC\) có:
AC=BC (cmt)
\(\widehat {ACM} = \widehat {BCM}\) (cmt)
CM chung
\( \Rightarrow \Delta MAC = \Delta MBC\)(c.g.c)

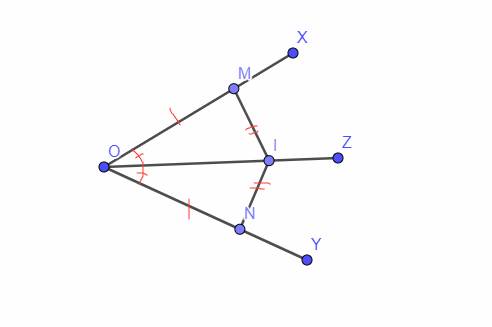
`a,` Xét Tam giác `OIM` và Tam giác `OIN` có:
`OM = ON (g``t)`
\(\widehat{MOI}=\widehat{NOI}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OI` chung
`=>` Tam giác `OIM =` Tam giác `OIN (c-g-c)`
`b,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`->` \(\widehat{OIM}=\widehat{OIN}\) `( 2` góc tương ứng `)`
`c,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`-> IM = IN (2` cạnh tương ứng `)`
`\color{blue}\text {#DuyNam}`
x O y z M I A B N K
Ta kéo dài tia MA , lấy điểm N thuộc tia MA sao cho IN = IK
Dễ thấy OAMB là hình vuông vì có góc O = góc B = góc A = 900 và OM là tia phân giác góc O . => OA = OB
Ta có : IN = IK (dựng hình) ; \(\widehat{NIO}=\widehat{OIK}\) (gt) ; IO là cạnh chung của hai tam giác NIO và OIK
=> \(\Delta NIO=\Delta IOK\left(c.g.c\right)\)=> \(\widehat{NOI}=\widehat{IOK}\) ; ON = OK
Xét hai tam giác vuông : \(\Delta AON\) và \(\Delta BOK\)có OA = OB (cmt) ; ON = OK (cmt)
=> \(\Delta AON=\Delta BOK\left(ch.cgv\right)\) => \(\widehat{AON}=\widehat{BOK}\)
Mà \(\widehat{BOK}+\widehat{AOK}=90^o\) \(\Rightarrow\widehat{AON}+\widehat{AOK}=90^o\)
hay \(\widehat{NOK}=2\widehat{IOK}=90^o\Rightarrow\widehat{IOK}=\frac{90^o}{2}=45^o\)
Cô ghi dấu góc ở đâu vậy