Tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD. a) Cm : AB = CD b) So sánh góc BAM và góc CAM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\widehat{C}=180^o-\widehat{A}-\widehat{B}=180^o-80^o-60^o=40^o\)
Có \(\widehat{C}< \widehat{B}< \widehat{A}\) suy ra \(AB< AC< BC\).
Xét tứ giác \(ABDC\) có hai đường chéo \(AD,BC\) cắt nhau tại trung điểm mỗi đường nên \(ABDC\) là hình bình hành.
Suy ra \(AB=CD\).
\(AB+AC=AB+CD>AD\) (bất đẳng thức tam giác trong tam giác \(ACD\))
Xét tam giác \(ACD\) có hai trung tuyến \(AN,CM\) cắt nhau tại \(K\) nên \(K\) là trọng tâm tam giác \(ACD\) suy ra \(CK=\dfrac{2}{3}CM\).
Mà \(BC=2CM\) suy ra \(BC=3CK\).

a: Xet ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b; góc BAM=góc CDA
mà góc CDA>góc CAM
nên góc BAM>góc CAM

a, áp dụng định lí pytago vào tam giác ABC ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=3^2+4^2=25\)
\(BC=\sqrt{25}=5\)
B, xét tam giác BAC và DCA có:
BM=MC
AM=MD
góc BMA= DMC (đối đỉnh)
=> Tam giác BAC=DCA
=>BA=DC
Góc BAM=MDC=>BA//DC(so le trong)
cho mk xin **** nah

a: góc C=180-80-60=40 độ
Vì góc A>góc B>góc C
=>BC>AC>AB
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AB=CD
AB+AC=AB+BD>AD
c: Xét ΔADC có
AN,CM là trung tuyến
AN cắt CM tại K
=>K là trọng tâm
=>CK=2/3CM=2/3*1/2BC=1/3CB
=>BC=3CK

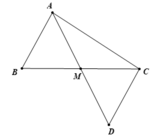
c. Trong tam giác ADC có CD < AC ⇒ ∠(DAC) < ∠(ADC) (1 điểm)
Mà ∠(BAM) = ∠(ADC) ( 2 góc tương ứng vì ΔABM = ΔDCM) (0.5 điểm)
Suy ra ∠(MAB) > ∠(MAC) (0.5 điểm)

`a)`
`Delta ABC` có :
`hat(BAC)+hat(C_1)+hat(B)=180^0` ( đlý )
hay `80^0+hat(C_1)+60^0=180^0`
`=>hat(C_1)=40^0`
mà `hat(B)>hat(C_1)(60^0>40^0)`
nên `AC>AB`( Qhệ giữa góc và cạnh đối diện trong `Delta` )
`b)`
Có `M` là tđ của `BC`
`=>MB=MC`
Xét `Delta ABM` và `Delta CDM` có :
`{:(AM=DM(GT)),(hat(M_1)=hat(M_2)(đối.đỉnh)),(BM=MC(cmt)):}}`
`=>Delta ABM=Delta CDM(c.g.c)`
`=>AB=CD` ( 2 cạnh t/ứng )(đpcm)
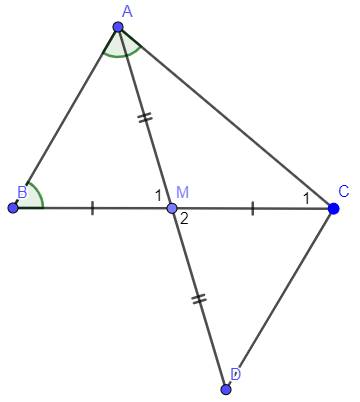
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hbh
=>AB=CD
b: ABDC là hbh
=>AB//CD
AB=CD
AB<AC
=>CD<AC
=>góc CAD<góc CDA
=>góc CAD<góc BAD