cho tam giác ABC cân AB=10cm,HC=6cm ,a) tính AH ,B)kẻ HK vuông góc với AB, k thuộc AB ,HI vuông góc với AC I thuộc AC Chứng minh tam giác AKI cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MA
10 tháng 5 2015
a) Vì trong tam giác cân đường cao đông thời là trung tuyến ;trung trực ,...
Nên AH là đường cao đồng thời là trugn tuyến ứng với canh BC
=>HB=HC
b) Ta có HB+HC=BC
=>HB=HC=BC/2=8/2=4cm
Ap dụng định lí Py-ta-go vào tam giác BAH ta có
AH2+BH2=AB2
AH2=AB2-BH2
AH2= 52-42
AH2=25-16=9
=>AH=3
C)Xét tam giác vuông BDH và CEH ta có
HB=HC(theo câu a)
Góc B=C(Vì tam giác ABC cân ở A)
=>tam giác BDH=CEH(ch-gn)
=>HD=HE(tương ứng)
Vậy tam giác HDE có HD=HE nên cân ở H
21 tháng 7 2023
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
HB=15^2/25=9cm
HC=25-9=16cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=25/7
=>BD=75/7cm; CD=100/7cm
b: ΔAHB vuông tại H có HI là đường cao
nên AI*AB=AH^2
ΔAHC vuông tại H có HK là đường cao
nên AK*AC=AH^2
=>AI*AB=AK*AC
c: AI*AB=AK*AC
=>AI/AC=AK/AB
=>ΔAIK đồng dạng với ΔACB
11 tháng 2 2016
a) Vì tam giác ABC cân => góc B = góc C
Xét tam giác ABH và tam giác ACH có:
AB = AC ( gt )
góc B = góc C ( cmt )
AH là cạnh chung
=> tam giác ABH = tam giác ACH ( c.g.c )
=> HB = HC ( hai cạnh tương ứng )
b) Vì HB = HC ( cmt )
Mà HB + HC = 8 cm => HB = HC = 8/2 = 4 cm
Xét tam giác ABH vuông tại H có:
AH mũ 2 + BH mũ 2 = AB mũ 2 ( pitago )
AH mũ 2 + 4 mũ 2 = 5 mũ 2
AH mũ 2 + 16 = 25
AH mũ 2 = 25 - 16
AH mũ 2 = 9
=> AH = căn bậc 2 của 9 = 3 cm
c) Mình bó tay :P
d. Có tam giác DHB = tam giác EHC ( cạnh huyền-góc nhọn)
=) HD = HE (tương ứng)
Mà trong tam giác vuông HEC, HC lớn nhất và (cạnh huyền)> HE (cạnh góc vuông)
=) HD<HC
11 tháng 2 2016
a) Vì tam giác ABC cân => góc B = góc C
Xét tam giác ABH và tam giác ACH có:
AB = AC ( gt )
góc B = góc C ( cmt )
AH là cạnh chung
=> tam giác ABH = tam giác ACH ( c.g.c )
=> HB = HC ( hai cạnh tương ứng )
b) Vì HB = HC ( cmt )
Mà HB + HC = 8 cm => HB = HC = 8/2 = 4 cm
Xét tam giác ABH vuông tại H có:
AH mũ 2 + BH mũ 2 = AB mũ 2 ( pitago )
AH mũ 2 + 4 mũ 2 = 5 mũ 2
AH mũ 2 + 16 = 25
AH mũ 2 = 25 - 16
AH mũ 2 = 9
=> AH = căn bậc 2 của 9 = 3 cm
d. Có tam giác DHB = tam giác EHC ( cạnh huyền-góc nhọn)
=> HD = HE (tương ứng)
Mà trong tam giác vuông HEC, HC lớn nhất và (cạnh huyền)> HE (cạnh góc vuông)
=> HD<HC
10 tháng 3 2023
`a)`
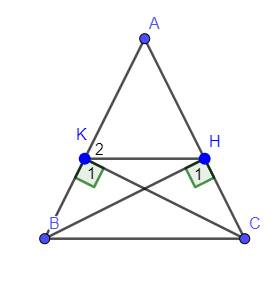
+, Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=hat(ACB)`
hay `hat(KBC)=hat(HCB)`
Xét `Delta BHC` và `Delta CKB` có :
`{:(hat(H_1)=hat(K_1)(=90^0)),(BC-chung),(hat(HCB)=hat(KBC)(cmt)):}}`
`=>Delta BHC=Delta CKB(c.h-g.n)(đpcm)`
+, Có `Delta BHC=Delta CKB(cmt)`
`=>HC=BK` ( 2 cạnh t/ứng )
mà `AB=AC(Delta ABC` cân tại `A)`
nên `AB-BK=AC-CH`
hay `AK=AH`
`=>Delta AHK` cân tại `A(đpcm)`
`b)`
Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=(180^0-hat(A))/2` (1)
`Delta AHK ` cân tại `A(cmt)=>hat(K_2)=(180^0-hat(A))/2` (2)
Từ (1) và (2) suy ra :
`hat(ABC)=hat(K_2)`
mà `2` góc này ở vị trí Đồng vị
nên `KH////BC(đpcm)`
các bạn ơi giúp mình với ạ nhờ các bạn giúp nhanh chứ mai mình thi rồi
mau
đề có đúng ko bn