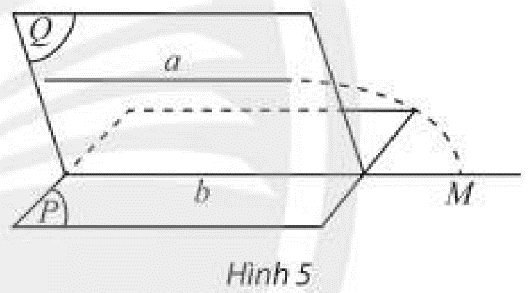
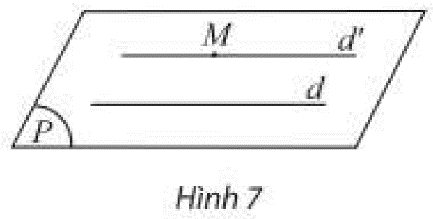
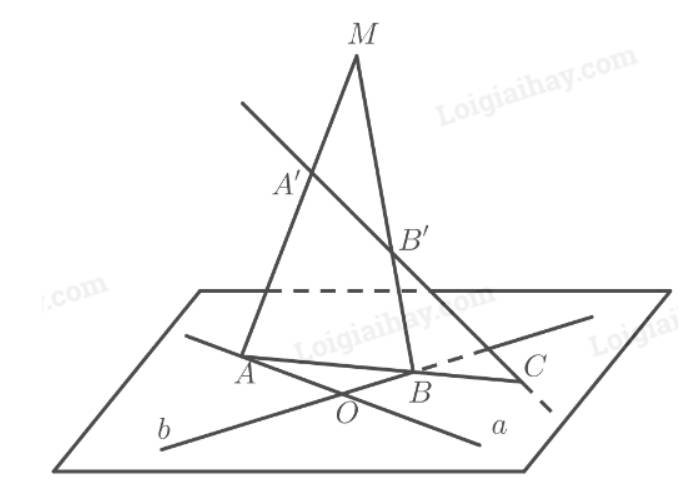
Cho một mặt phẳng \(\left(P\right)\),một điểm A\(\in\)mp\(\left(P\right)\) và một đường thẳng \(d\)// mp\(\left(P\right)\).Đường thẳng d và điểm A xác định một \(mp\left(Q\right)\).Chứng tỏ hai mặt ph...

KN

Khải Nhi

5 tháng 8 2016 - olm

Cho một mặt phẳng \(\left(P\right)\),một điểm A\(\in\)mp\(\left(P\right)\) và một đường thẳng \(d\)// mp\(\left(P\right)\).Đường thẳng d và điểm A xác định một \(mp\left(Q\right)\).Chứng tỏ hai mặt phẳng \(\left(P\right)\)và \(\left(Q\right)\) cắt nhau theo giao tuyến \(d'\)Chứng...

Đọc tiếp

#Toán lớp 8

1

LK

Lee Kiên

6 tháng 8 2016

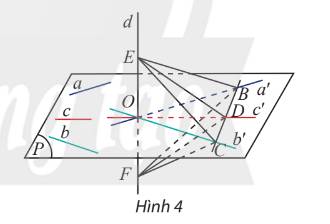
Ta có mp P và Q cùng đi qua A, hai mp có giao điểm thì cắt nhau.

Với d và d' thuộc Q cùng với việc d song song mp P(mp chứa d') suy ra d song song d'.

Nếu d song song mp P mà d và d' ko cùng thuộc một mp thì đây là hai đừờng thẳng chéo nhau

Đúng(0)

B

Buddy

17 tháng 7 2023

Cho đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và \(a\) song song với một đường thẳng \(b\) nằm trong \(\left( P \right)\). Đặt \(\left( Q \right) = mp\left( {a,b} \right)\).a) Tìm giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).b) Giả sử \(a\) có điểm chung \(M\) với \(\left( P \right)\) thì điểm \(M\) phải nằm trên đường thẳng nào? Điều này có trái với giả thiết \(a\parallel b\)...

Đọc tiếp

#Toán lớp 11

1

QT

Quoc Tran Anh Le

Giáo viên

22 tháng 9 2023

a) Ta có:

\(\left. \begin{array}{l}b \subset \left( P \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow b = \left( P \right) \cap \left( Q \right)\)

Vậy \(b\) là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).

b) Ta có:

\(\left. \begin{array}{l}M \in a\\a \subset \left( Q \right)\end{array} \right\} \Rightarrow M \in \left( Q \right)\)

Lại có: \(M \in \left( P \right)\)

Do đó điểm \(M\) nằm trên giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Vậy \(M \in b\).

Vậy \(M\) là một điểm chung của hai đường thẳng \(a\) và \(b\), trái với giả thiết \(a\parallel b\).

Đúng(0)

B

Buddy

17 tháng 7 2023

a) Trong không gian, cho điểm \(M\) ở ngoài đường thẳng \(d\). Đặt \(\left( P \right) = mp\left( {M,d} \right)\). Trong \(\left( P \right)\), qua \(M\) vẽ đường thẳng \(d'\) song song với \(d\), đặt \(\left( Q \right) = mp\left( {d,d'} \right)\). Có thể khẳng định hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) trùng nhau không?b) Cho ba mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) cắt nhau theo ba giao tuyến \(a,b,c\)...

Đọc tiếp

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

22 tháng 9 2023

a) Theo đề bài ta có: \(d' \subset \left( P \right),d' \subset \left( Q \right)\) nên \(d'\) là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).

Lại có: \(d \subset \left( P \right),d \subset \left( Q \right)\) nên \(d\) cũng là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).

Theo tính chất thừa nhận 5: hai mặt phẳng phân biệt có một đường thẳng chung duy nhất. Vậy hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) trùng nhau.

b) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}M \in a\\a \subset \left( P \right)\end{array} \right\} \Rightarrow M \in \left( P \right)\\\left. \begin{array}{l}M \in b\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow M \in \left( Q \right)\end{array}\)

Do đó điểm \(M\) nằm trên giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Vậy \(M \in c\).

Đúng(0)

B

Buddy

13 tháng 8 2023

Cho góc nhị diện có hai mặt là hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cạnh của góc nhị diện là đường thẳng \(d\).Qua một điểm \(O\) trên đường thẳng \(d\), ta kẻ hai tia \(Ox,Oy\) lần lượt thuộc hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cùng vuông góc với đường thẳng \(d\). Góc \(xOy\) gọi là góc phẳng nhị diện của góc nhị diện đã cho (Hình 38).Giả sử góc \(x'Oy'\) cũng là góc...

Đọc tiếp

#Toán lớp 11

1

QT

Quoc Tran Anh Le

Giáo viên

22 tháng 9 2023

Trong \(\left( P \right)\) ta có:

\(\left. \begin{array}{l}Ox \bot d\\O'x' \bot d\end{array} \right\} \Rightarrow Ox\parallel O'x'\)

Trong \(\left( Q \right)\) ta có:

\(\left. \begin{array}{l}Oy \bot d\\O'y' \bot d\end{array} \right\} \Rightarrow Oy\parallel O'y'\)

Vậy \(\left( {Ox,Oy} \right) = \left( {O'x',O'y'} \right)\) hay số đo của hai góc \(xOy\) và \(x'Oy'\) bằng nhau.

Đúng(0)

B

Buddy

17 tháng 7 2023

Cho hai đường thẳng \(a\) và \(b\) cắt nhau tại \(O\) và điểm \(M\) không thuộc \(mp\left( {a,b} \right)\).a) Tìm giao tuyến của hai mặt phẳng \(\left( {M,a} \right)\) và \(\left( {M,b} \right)\).b) Lấy \(A,B\) lần lượt là hai điểm trên \(a,b\) và khác với điểm \(O\). Tìm giao tuyến của \(\left( {MAB} \right)\) và \(mp\left( {a,b} \right)\).c) Lấy điểm \(A'\) trên đoạn \(MA\) và điểm \(B'\) trên đoạn \(MB\) sao cho đường thẳng...

Đọc tiếp

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

22 tháng 9 2023

a) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}M \in \left( {M,a} \right)\\M \in \left( {M,b} \right)\end{array} \right\} \Rightarrow M \in \left( {M,a} \right) \cap \left( {M,b} \right)\\\left. \begin{array}{l}O \in a \subset \left( {M,a} \right)\\O \in b \subset \left( {M,b} \right)\end{array} \right\} \Rightarrow O \in \left( {M,a} \right) \cap \left( {M,b} \right)\end{array}\)

Vậy giao tuyến của hai mặt phẳng \(\left( {M,a} \right)\) và \(\left( {M,b} \right)\) là đường thẳng \(MO\).

b) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {MAB} \right)\\A \in a \subset \left( {a,b} \right)\end{array} \right\} \Rightarrow A \in \left( {MAB} \right) \cap \left( {a,b} \right)\\\left. \begin{array}{l}B \in \left( {MAB} \right)\\B \in b \subset \left( {a,b} \right)\end{array} \right\} \Rightarrow B \in \left( {MAB} \right) \cap \left( {a,b} \right)\end{array}\)

Vậy giao tuyến của hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {a,b} \right)\) là đường thẳng \(AB\) (1).

c) Ta có:

\(\left. \begin{array}{l}A' \in MA \subset \left( {MAB} \right)\\B' \in MB \subset \left( {MAB} \right)\end{array} \right\} \Rightarrow A'B' \subset \left( {MAB} \right)\)

Vì \(C \in A'B' \subset \left( {MAB} \right)\) và \(C \in mp\left( {a,b} \right)\) nên điểm \(C\) nằm trên giao tuyến của hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {a,b} \right)\) (2).

Từ (1) và (2) suy ra ba điểm \(A,B,C\) thẳng hàng.

Đúng(1)

SG

Sách Giáo Khoa

23 tháng 5 2017

Trong các mệnh đề sau đây, mệnh đề nào đúng ? Mệnh đề nào sai ? a) Cho hai đường thẳng a và b song song với nhau. Nếu có một đường thẳng d vuông góc với a thì d vuông góc với b b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau c) Một mặt phẳng \(\left(\alpha\right)\) và một đường thẳng a cùng vuông góc với đường thẳng b thì a...

Đọc tiếp

#Toán lớp 11

1

NT

Nguyen Thuy Hoa

26 tháng 5 2017

a) Đúng

b) Đúng

c) Sai

d) Sai

e) Sai

Đúng(0)

SG

Sách Giáo Khoa

23 tháng 5 2017

Cho tam giác đều ABC có cạnh bằng a. Đường thẳng d vuông góc với mp (ABC) tại A và \(M\in\left(d\right)\). Gọi H, O lần lượt là trực tâm của tam giác ABC và tam giác MBC. Gọi N là giao điểm của HO và d. Chứng minh :

\(MC\perp mp\left(BOH\right);HO\perp mp\left(MBC\right)\)

#Toán lớp 11

1

NT

Nguyen Thuy Hoa

25 tháng 5 2017

Vectơ trong không gian, Quan hệ vuông góc

Gọi I, J, K lần lượt là các giao điểm của AH và MO; AC và BH; MC và BO

\(MA\perp\left(ABC\right)\Rightarrow MA\perp BJ\)

H là trực tâm của tam giác ABC => \(AC\perp BJ\)

\(\left\{{}\begin{matrix}BJ\perp MA\\BJ\perp AC\end{matrix}\right.\)\(\Rightarrow BJ\perp\left(MAC\right)\)

\(\Rightarrow BJ\perp MC\)

O là trực tâm của tam giác MBC nên \(BO\perp MC\)

Do đó : \(BO\perp\left(BJK\right)\Rightarrow MC\perp\left(BOH\right)\Rightarrow MC\perp OH\) (1)

Chứng minh tương tự : \(MB\perp OH\) (2)

Từ (1) và (2) cho \(OH\perp\left(MBC\right)\)

Đúng(0)

B

Buddy

17 tháng 7 2023

Cho hình bình hành \(ABCD\) và một điểm \(S\) không nằm trong mặt phẳng \(\left( {ABCD} \right)\). Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là một đường thẳng song song với đường thẳng nào sau đây?

A. \(AB\).

B. \(AC\).

C. \(BC\).

D. \(SA\).

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

22 tháng 9 2023

Ta có:

\(\left. \begin{array}{l}S \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\\A{\rm{B}}\parallel C{\rm{D}}\\AB \subset \left( {SAB} \right)\\C{\rm{D}} \subset \left( {SC{\rm{D}}} \right)\end{array} \right\}\)

\( \Rightarrow \)Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là đường thẳng \(d\) đi qua \(S\), song song với \(AB\) và \(C{\rm{D}}\).

Chọn A.

Đúng(0)

B

Buddy

17 tháng 7 2023

Trong mặt phẳng \(\left( P \right)\) cho hình bình hành \(ABCD\). Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với \(\left( P \right)\) lần lượt đi qua các điểm \(A,B,C,D\). Một mặt phẳng \(\left( Q \right)\) cắt bốn nửa đường thẳng nói trên tại \(A',B',C',D'\). Chứng minh rằng:\(AA' + CC' = BB' +...

Đọc tiếp

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

22 tháng 9 2023

a) Ta có:

\(\left. \begin{array}{l}AA'\parallel DD'\\DD' \subset \left( {CC'D'D} \right)\end{array} \right\} \Rightarrow AA'\parallel \left( {CC'D'D} \right)\)

\(\left. \begin{array}{l}AB\parallel C{\rm{D}}\\C{\rm{D}} \subset \left( {CC'D'D} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {CC'D'D} \right)\)

\(\left. \begin{array}{l}AA'\parallel \left( {CC'D'D} \right)\\AB\parallel \left( {CC'D'D} \right)\\AA',AB \subset \left( {AA'B'B} \right)\end{array} \right\} \Rightarrow \left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\)

\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( P \right) \cap \left( {AA'B'B} \right) = A'B'\\\left( P \right) \cap \left( {CC'D'D} \right) = C'D'\end{array} \right\} \Rightarrow A'B'\parallel C'D'\left( 1 \right)\)

\(\left. \begin{array}{l}AD\parallel BC\\BC \subset \left( {BB'C'C} \right)\end{array} \right\} \Rightarrow AD\parallel \left( {BB'C'C} \right)\)

\(\left. \begin{array}{l}AA'\parallel BB'\\BB' \subset \left( {BB'C'C} \right)\end{array} \right\} \Rightarrow AA'\parallel \left( {BB'C'C} \right)\)

\(\left. \begin{array}{l}AA'\parallel \left( {BB'C'C} \right)\\AD\parallel \left( {BB'C'C} \right)\\AA',AD \subset \left( {AA'D'D} \right)\end{array} \right\} \Rightarrow \left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\)

\(\left. \begin{array}{l}\left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\\\left( P \right) \cap \left( {AA'D'D} \right) = A'D'\\\left( P \right) \cap \left( {BB'C'C} \right) = B'C'\end{array} \right\} \Rightarrow A'D'\parallel B'C'\left( 2 \right)\)

Từ (1) và (2) suy ra \(A'B'C'D'\) là hình bình hành.

Gọi \(O = AC \cap B{\rm{D}},O' = A'C' \cap B'{\rm{D}}'\)

\( \Rightarrow O\) là trung điểm của \(AC,B{\rm{D}}\), \(O'\) là trung điểm của \(A'C',B'{\rm{D}}'\).

\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( {AA'C'C} \right) \cap \left( {AA'B'B} \right) = AA'\\\left( {AA'C'C} \right) \cap \left( {CC'D'D} \right) = CC'\end{array} \right\} \Rightarrow AA'\parallel CC'\)

\( \Rightarrow AA'C'C\) là hình thang

\(O\) là trung điểm của \(AC\)

\(O'\) là trung điểm của \(A'C'\)

\( \Rightarrow OO'\) là đường trung bình của hình thang \(AA'C'C\)

\( \Rightarrow AA' + CC' = 2OO'\left( 3 \right)\)

\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( {BB'D'D} \right) \cap \left( {AA'B'B} \right) = BB'\\\left( {BB'D'D} \right) \cap \left( {CC'D'D} \right) = DD'\end{array} \right\} \Rightarrow BB'\parallel DD'\)

\( \Rightarrow BB'D'D\) là hình thang

\(O\) là trung điểm của \(B{\rm{D}}\)

\(O'\) là trung điểm của \(B'D'\)

\( \Rightarrow OO'\) là đường trung bình của hình thang \(BB'D'D\)

\( \Rightarrow BB' + DD' = 2OO'\left( 4 \right)\)

Từ (3) và (4) suy ra \(AA' + CC' = BB' + DD'\left( { = 2OO'} \right)\).

Đúng(0)

B

Buddy

20 tháng 8 2023

Cho đường thẳng \(d\) vuông góc với hai đường thẳng 2 cắt nhau \(a\) và \(b\) trong mặt phẳng \(\left( P \right)\). Xét một đường thẳng \(c\) bất kì trong \(\left( P \right)\) (\(c\) không song song với \(a\) và \(b\)). Gọi \(O\) là giao điểm của \(d\) và \(\left( P \right)\). Trong \(\left( P \right)\) vẽ qua \(O\) ba đường thẳng \(a',b',c'\) lần lượt song song với \(a,b,c\). Vẽ một đường thẳng cắt \(a',b',c'\) lần lượt...

Đọc tiếp