Vẽ hình ghi giả thiết, kết luận và chứng minh
Hai đường thẳng phân giác của 2 góc so le trong thì song song với nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
29 tháng 7 2019
\(\frac{3x-y}{x+y}=\frac{3}{4}\)
\(\Leftrightarrow4\left(3x-y\right)=3\left(x+y\right)\)
\(\Leftrightarrow12x-4y=3x+3y\)
\(\Leftrightarrow12x-4y-3x-3y=0\)
\(\Leftrightarrow9x-7y=0\)
\(\Leftrightarrow9x=7y\Leftrightarrow\frac{x}{7}=\frac{y}{9}\)
5 tháng 10 2021
Giả thiết: Hai đường thẳng song song
Kết luận: Các tia phân giác của mỗi cặp góc đồng vị song song với nhau
4 tháng 9 2016
mù ak, ghi dấu rùi ây! ko tl dc thì ra chỗ khác đỡ tốn chỗ giải toán
10 tháng 11 2021
Tham khảo!
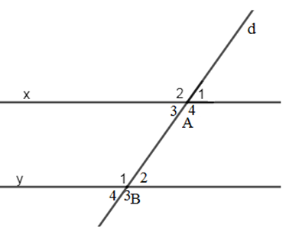
Giả thiết: Đường thẳng cắt hai đường thẳng sao cho có một góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.
9 tháng 11 2021
a: Giả thiết: a//b
Kết luận: \(\widehat{A_1}=\widehat{B_1}\)
Ta có: góc xAc và góc xBd so le trong
=> góc xAc= góc xBd
Am và An lần lượt là tia p/g của xAc và xBd
=> góc A1 = góc A2 = góc B1 = góc B2
Mà góc A1 và B1 ở vị trí đồng vị
=> Am // An
am // bn
ef cắt am, an lần lượt tại A , B.
Bc là phân giác góc 1 hay B1 = B2
Ad là phân giác goc A hay A1= A2
Ta có:
Góc bBe = góc fAm (2 góc so le trong, am // bn)
\(\frac{1}{2}bBe=\frac{1}{2}fAm\)(gt)
=> A1 = B1 ( so le trong)
Vậy Bc // Ad.