Tìm abcd biết
abcd - bcd . 2 = ac
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




abcd - bcd x 2 = ac
a x 1000 + bcd - bcd x 2 = a x 10 + c
a x 1000 - bcd = a x 10 + c
a x 990 - bcd = c
=> a = 1 ; b = 9 ; c = 8 hoặc 9
Nếu c = 9 => bcd = 990 - 9 = 981 (loại)
Vậy c= 8 => bcd = 990 - 8 = 982 => d = 2

a: Trong mp(ABC), gọi E là giao điểm của MN và BC
\(O\in\left(OMN\right);O\in\left(BCD\right)\)
=>\(O\in\left(OMN\right)\cap\left(BCD\right)\)
\(E\in MN\subset\left(OMN\right);E\in BC\subset\left(BCD\right)\)
=>\(E\in\left(OMN\right)\cap\left(BCD\right)\)
Do đó: \(\left(OMN\right)\cap\left(BCD\right)=OE\)
b: Chọn mp(BCD) có chứa DB
\(\left(OMN\right)\cap\left(BCD\right)=OE\)
Gọi F là giao của OE với DB
=>F là giao của DB với mp(OMN)
Chọn mp(BCD) có chứa DC
\(\left(OMN\right)\cap\left(BCD\right)=OE\)
Gọi K là giao của OE với DC
=>K là giao của DC với mp(OMN)

1/ \(\overrightarrow{AM}=3\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MG}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MA}+3\overrightarrow{AG}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AM}=3\overrightarrow{AG}\)
Ban tu ket luan
2/ Bạn coi lại đề bài, đẳng thức kia có vấn đề. 2k-1IB??
\(\overrightarrow{IA}+2k-1+\overrightarrow{IB}+k\overrightarrow{IC}+\overrightarrow{ID}=0\)

Đáp án D
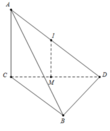
Gọi M là trung điểm của CD đường thẳng qua M song song với AC cắt AD tại trung điểm I của AD. Khi đó I là tâm mặt cầu ngoại tiếp khối tứ diện

cần sửa a,b,c, d là các số tự nhiên < 10, không nên viết abc < 10
abcd=1882