Trong cùng mặt phẳng tọa độ cho [P] : y= -1/4 x2 và [d] : y=x+1
A/ Vẽ [P] và [d] trên cùng mặt phẳng tọa độ
B/Tìm tọa độ giao điểm của [P] và [d] bằng phép tính : hệ pt 3x-y=5 và 2x+3y=18
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 11 2021
\(b,\text{PT hoành độ giao điểm: }2x-5=-\dfrac{1}{2}x\Leftrightarrow\dfrac{5}{2}x=5\Leftrightarrow x=2\Leftrightarrow y=-1\Leftrightarrow M\left(2;-1\right)\)
Y
21 tháng 3 2023
\(a,\) Tự vẽ nha
\(b,\) Gọi \(A\left(x_A;y_A\right)\) ; \(B\left(x_B;y_B\right)\) là tọa độ giao điểm của (P) và (D)
Ta có :
\(-x^2=x-2\)
\(\Leftrightarrow-x^2-x+2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=1\\x_2=-2\end{matrix}\right.\)
Thay \(x_1=1\) vào (p) : \(y=-x^2\Rightarrow y=-1^2=-1\)
Thay \(x_2=-2\) vào (d) : \(y=x-2\Rightarrow y=-2-2=-4\)
Vậy tọa độ của 2 đồ thị hs là : \(A\left(1;-1\right);B\left(-2;-4\right)\)
14 tháng 7 2023
a: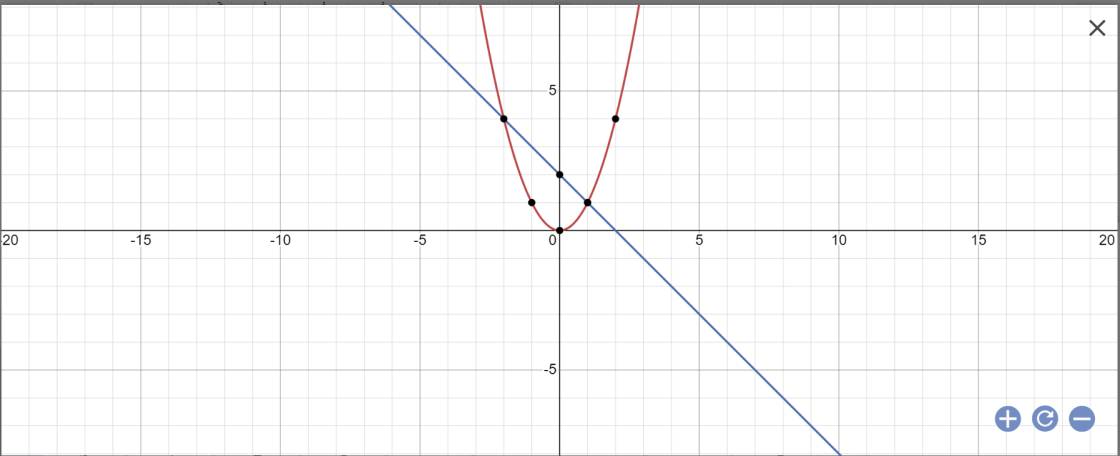 
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
22 tháng 12 2023
a:
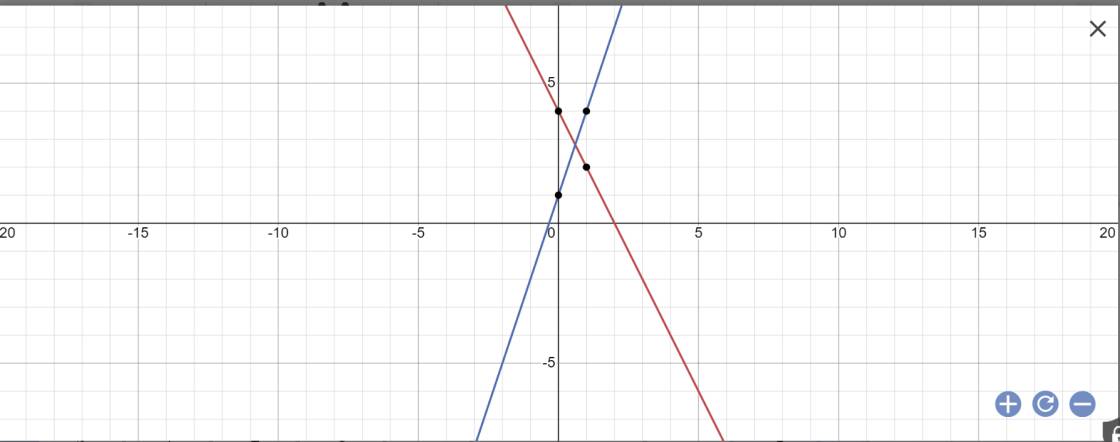
b: Phương trình hoành độ giao điểm là:
4-2x=3x+1
=>-2x-3x=1-4
=>-5x=-3
=>\(x=\dfrac{3}{5}\)
Thay x=3/5 vào y=3x+1, ta được:
\(y=3\cdot\dfrac{3}{5}+1=\dfrac{9}{5}+1=\dfrac{14}{5}\)
Vậy: \(N\left(\dfrac{3}{5};\dfrac{14}{5}\right)\)
c: (d'): y=3x+1
=>a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^034'\)
26 tháng 3 2023
a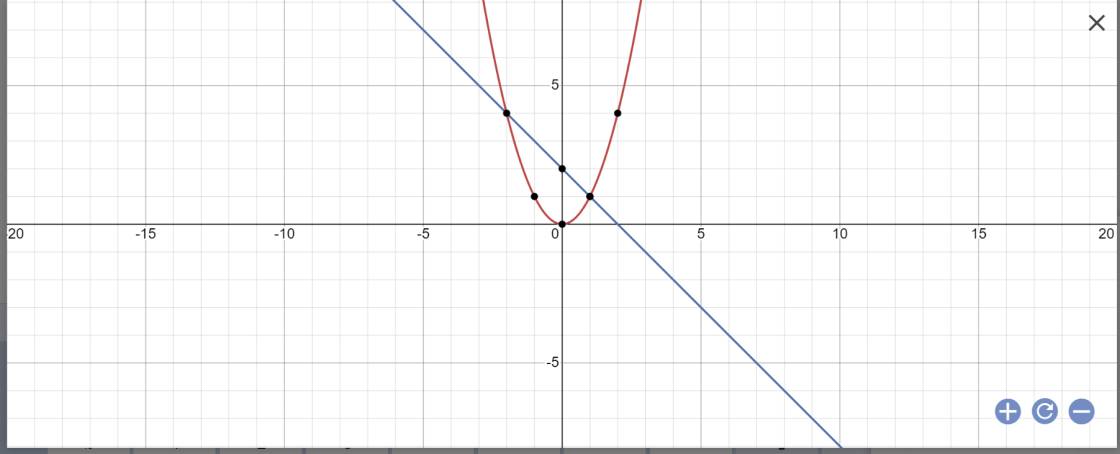
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
24 tháng 11 2021
\(b,\text{PT hoành độ giao điểm: }-2x+5=x-1\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\\ \text{Vậy }A\left(2;1\right)\text{ là giao điểm }\left(d_1\right)\text{ và }\left(d_2\right)\\ c,\text{Gọi }\left(d_3\right):y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \left(d_3\right)\text{//}\left(d_1\right)\text{ và }M\left(-2;1\right)\in\left(d_3\right)\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne5\\-2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\\ \Leftrightarrow\left(d_3\right):y=-2x-1\)
12 tháng 5 2023
b: PTHĐGĐ là:
-1/2x^2=1/2x-1
=>-x^2=x-2
=>-x^2-x+2=0
=>x^2+x-2=0
=>x=-2 hoặc x=1
=>y=-1/2*4=-2 hoặc y=-1/2
a: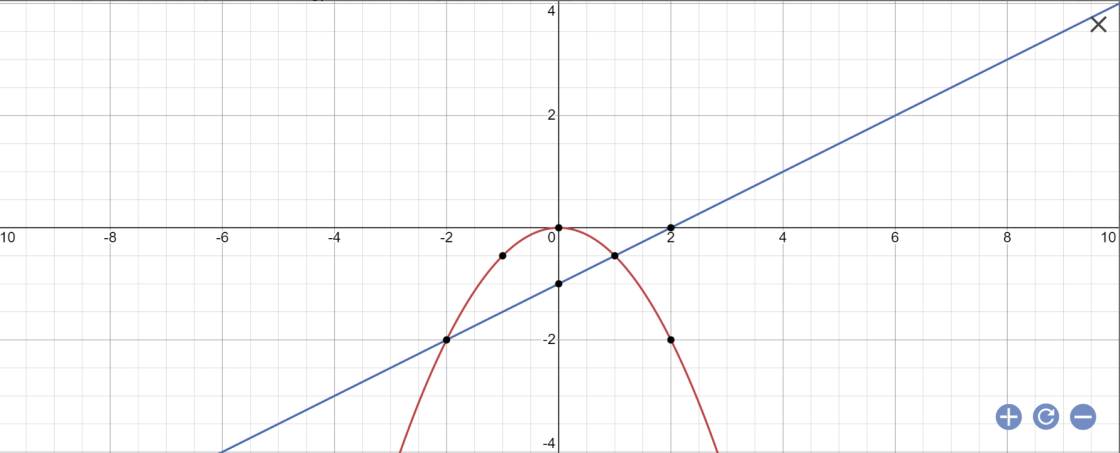 
NA
Nguyễn An Ninh
VIP
12 tháng 5 2023
b. ta có phương trình hoành độ: 1/2.x^2=3/2.x-1 <=>1/2.x^2-3/2.x+1=0 <=> x^2-3x+2=0
Δ=1>0 =>pt có hai nghiệm phân biệt
x=2 =>y=2 =>A (2;2)
x=1 =>y=1/2 =>B(1;1/2)
Vậy (P)và (d) cắt nhau tại hai điểm A(2;2) và B(1;1/2)
31 tháng 10 2021
b, PT hoành độ giao điểm: \(2x-5=-\dfrac{1}{2}x\Leftrightarrow x=2\Leftrightarrow y=-\dfrac{1}{2}\cdot2=-1\)
\(\Leftrightarrow A\left(2;-1\right)\)
Vậy A(2;-1) là tọa độ giao điểm 2 đths
1:
a: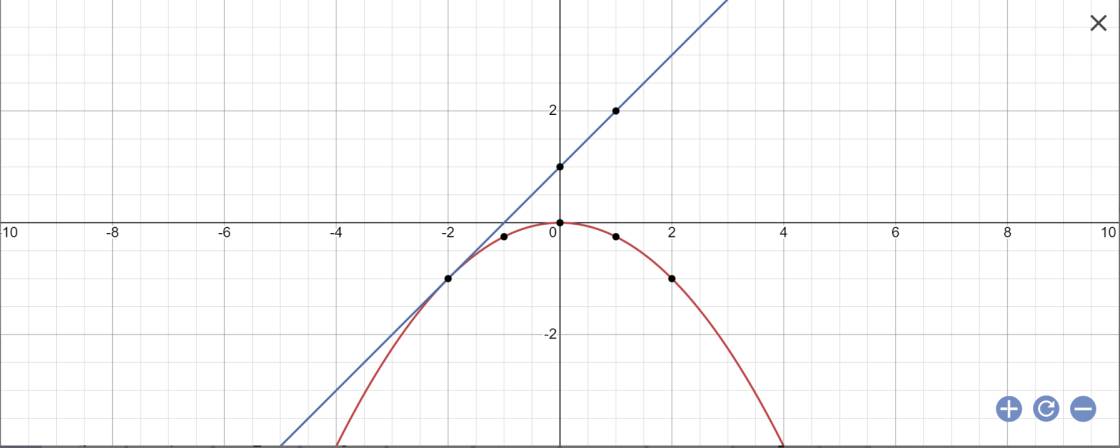
b: PTHĐGĐ là:
-1/4x^2-x-1=0
=>x^2+4x+4=0
=>(x+2)^2=0
=>x=-2
=>y=-1/4*(-2)^2=-1
2: 3x-y=5 và 2x+3y=18
=>9x-3y=15 và 2x+3y=18
=>11x=33 và 3x-y=5
=>x=3 và y=3*3-5=4