Cho tam giác ABC nội tiếp (O). Tiếp tuyến tại A của (O) cắt BC tại P
a) Giả sử (BCA) ̂=〖30〗^0. Tính số đo cung nhỏ và cung lớn AB, số đo (PAB) ̂ , số đo (AOB) ̂
b) Chứng minh
c) Tia phân giác trong góc A cắt BC và (O) lần lượt tại D và M. Chứng minh:
MB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

△ABC cân tại C
\(\Rightarrow\widehat{A}=\widehat{B}=\dfrac{180^o-\widehat{C}}{2}=\dfrac{180^o-40^o}{2}=70^o\)
A là góc nội tiếp chắn cung BC nhỏ
=> sdBC nhỏ = 2A= 2.70=140 độ

khi tia OA cắt đường tròn tâm O tại D nên AD là đường kính chia ra 2 cung AD bằng nhau
mà tam giác ABC cân tại A có góc ABC =góc ACB là 2 góc nội tiếp chắc 2 cung AB và AC nên cung AB=cung AC
cung AD=cung AB+cung BD
cung AD=cung AC+cung CD
ta có cung AD=cung AD,cung AB=AC=>cung BD=cung CD
theo đề bài số đo cung nhỏ BD=cung BD+cung CD=>100=2 cung CD=>cung CD bằng 50 độ
MÀ GÓC COD là góc ở tâm chắc cung CD
NÊN SUY RA ĐƯỢC GÓC COD BẰNG 50 ĐỘ

a: ΔOAC cântại O
mà OI là trung tuyến
nên OI vuông góc AC
góc OIE+góc OBE=180 độ
=>OIEB nội tiếp
b: góc ACB=1/2*180=90 độ
=>CB vuông góc AE
=>EB^2=EC*EA
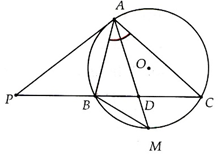
a: sđ cung nhỏ AB=2*30=60 độ
sđ cung lớn AB là 360-60=300 độ
góc PAB=góc BCA=30 độ
góc AOB=sđ cung nhỏ AB=60 độ
b,c: Bạn ghi lại đề đi bạn