Câu 11,12 ạ 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 1 2023
Câu 11:
b: -x^2+x-m<=0 với mọi x
Δ=1^2-4*(-1)*(-m)=1-4m
Để BPT luôn đúng thì 1-4m<=0 và -1<0
=>4m>=1
=>m>=1/4
c: mx^2+mx-1>=0
TH1: m=0
=>-1>=0(vô lý)
=>Nhận)
TH2: m<>0
Δ=m^2-4*m*(-1)=m^2+4m
Để BPT vô nghiệm thì m^2+4m<=0 và m<0
=>-4<=m<=0 và m<0
=>-4<=m<0
4 tháng 3 2023
Bài 12:
a: Để 12/3n-1 là số nguyên thì \(3n-1\in\left\{1;-1;2;-2;3;-3;4;-4;6;-6;12;-12\right\}\)
mà n nguyên
nên \(3n-1\in\left\{-1;2;-4\right\}\)
=>\(n\in\left\{0;1;-1\right\}\)
b: Để đay là số nguyên thì 2n+3=7k
=>2n=7k-3
=>\(n=\dfrac{7k-3}{2}\left(k\in Z\right)\)
c: Để đây là số nguyên thì 2n-6+11 chia hết cho n-3
=>\(n-3\in\left\{1;-1;11;-11\right\}\)
=>\(n\in\left\{4;2;14;-8\right\}\)
28 tháng 12 2021
Bài 10:
e: \(\Leftrightarrow x\left(x+2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
14 tháng 11 2023
Bài 11:
Gọi số học sinh giỏi 4 khối lần lượt là $a,b,c,d$ (em)
Theo bài ra ta có: $a+b+c-d=168$ và $\frac{a}{13}=\frac{b}{12}=\frac{c}{14}=\frac{d}{15}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{13}=\frac{b}{12}=\frac{c}{14}=\frac{d}{15}=\frac{a+b+c-d}{13+12+14-15}=\frac{168}{24}=7$
$\Rightarrow a=13.7=91; b=12.7=84; c=14.7=98; d=15.7=105$
AH
Akai Haruma
Giáo viên
14 tháng 11 2023
Bài 12:
Gọi số học sinh ba khối lần lượt là $a,b,c$ (học sinh).
Theo bài ra ta có: $\frac{a}{10}=\frac{b}{9}=\frac{c}{8}$ và $a-b=50$
Áp dụng TCDTSBN:
$\frac{a}{10}=\frac{b}{9}=\frac{c}{8}=\frac{a-b}{10-9}=\frac{50}{1}=50$
$\Rightarrow a=50.10=500; b=50.9=450; c=50.8=400$ (hs)
22 tháng 1 2022
TRẢ LỜI:
Vì phân số có tử số, mẫu số là số lẻ lớn hơn 6 nhỏ hơn 10. Vậy tử số đó có thể là 7 và 9.
a) Phân số đó bé hơn 1. Vậy phân số đó là 
b) Phân số đó bằng 1. Vậy phân số đó là 
c) Phân số đó lớn hơn 1. Vậy phân số đó là 
18 tháng 7 2021
11) \(8+\sqrt{60}=2\cdot4+2\cdot\sqrt{15}=2\left(4+\sqrt{15}\right)\)
12) \(11-\sqrt{72}=11-2\sqrt{18}=\left(3-\sqrt{2}\right)^2\)
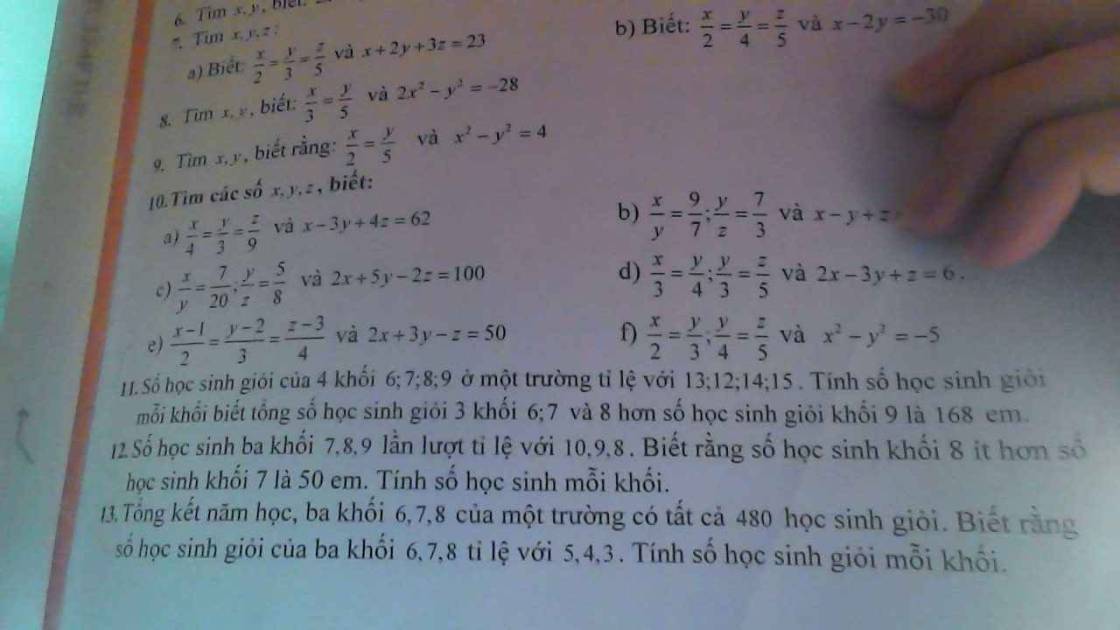
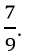
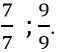
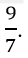
D
D
11.D
12.D