Cho A=2+22+23+...+22000
a,chứng minh A chia hết cho 31
b,tính A
c,Tìm x biết: 22x-1-2=A
giúp mk nha !!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 1 2021
Bài 3:
a) Ta có: \(C=2+2^2+2^3+...+2^{99}+2^{100}\)
\(=\left(2+2^2+2^3+2^4+2^5\right)+\left(2^6+2^7+2^8+2^9+2^{10}\right)+...+\left(2^{96}+2^{97}+2^{98}+2^{99}+2^{100}\right)\)
\(=2\left(1+2+2^2+2^3+2^4\right)+2^6\left(1+2+2^2+2^3+2^4\right)+...+2^{96}\left(1+2+2^2+2^3+2^4\right)\)
\(=31\cdot\left(2+2^6+...+2^{96}\right)⋮31\)(đpcm)
13 tháng 1 2021
Bài 1:
Ta có: \(A=3^{n+2}-2^{n+2}+3^n-2^n\)
\(=3^n\cdot9-2^n\cdot4+3^n-2^n\)
\(=3^n\left(9+1\right)-2^n\left(4+1\right)\)
\(=10\left(3^n-2^{n-1}\right)⋮10\)
Vậy: A có chữ số tận cùng là 0
Bài 2:
Ta có: \(abcd=1000\cdot a+100\cdot b+10\cdot c+d\)
\(\Leftrightarrow abcd=1000\cdot a+96\cdot b+8c+2c+4b+d\)
\(\Leftrightarrow abcd=8\left(125a+12b+c\right)+\left(2c+4b+d\right)\)
mà \(8\left(125a+12b+c\right)⋮8\)
và \(2c+4b+d⋮8\)
nên \(abcd⋮8\)(đpcm)
14 tháng 12 2022
a: \(=\left(1+2\right)+2^2\left(1+2\right)+...+2^{48}\left(1+2\right)\)
\(=3\left(1+2^2+...+2^{48}\right)⋮3\)
b: \(2^0+2^1+2^2+...+2^{101}\)
\(=\left(1+2+2^2\right)+...+2^{99}\left(1+2+2^2\right)\)
\(=7\left(1+...+2^{99}\right)⋮7\)
c: 2A=2+2^2+...+2^101
=>A=2^101-1
TH
23 tháng 6 2017
Ta thấy ràng 34=...1 , mà (......1)k luôn tận cùng là 1=> 4 thừa số 3 cho ta 1 tích tận cùng là 1 ;
- các hạng tử trong A liên tiếp cách đều 10 đơn vị nên :
Số hạng trong A là: (2013 -3):10 +1= 202 số;
=> Chia làm 202 : 4= 50 cặp sô(dư 2);
=> A= ...................1 x 3 x 3 =....................9;
Vậy A tận cùng là 9;
Xét B, ta có: 24=...6 , mà (...6)k luôn tận cùng là 6, nên
B có : (2012-2) : 10 +1 = 202 số hạng;
Chia làm : 202 : 4= 50 cặp (dư 2);
=> B=.................6 x 2 x 2=...............4;
=> A-B=......................9-........................4=.......................5;
Vậy x chia hết cho 5
14 tháng 6 2021
Giải:
a) \(A=1+2+2^2+2^3+...+2^{2021}\)
\(2A=2+2^2+2^3+2^4+...+2^{2022}\)
\(2A-A=\left(2+2^2+2^3+2^4+...+2^{2022}\right)-\left(1+2+2^2+2^3+...+2^{2021}\right)\)
\(A=2^{2022}-1\)
Vì \(2^{2022}>2^{2021}\) nên \(A>2^{2021}\)
b) Từ câu (a), ta có:
\(A=2^{2022}-1\)
\(A=2^{2020}.2^2-1\)
\(A=\left(2^4\right)^{505}.4-1\)
\(A=16^{505}.4-1\)
\(A=\left(\overline{...6}\right)^{505}.4-1\)
\(A=\overline{...6}.4-1\)
\(A=\overline{...4}-1\)
\(A=\overline{...3}\)
Vậy chữ số tận cùng của A là 3
c) Ta có:
\(A=1+2+2^2+2^3+...+2^{2021}\)
\(A=1.\left(1+2\right)+2^2.\left(1+2\right)+...+2^{2020}.\left(1+2\right)\)
\(A=1.3+2^2.3+...+2^{2020}.3\)
\(A=3.\left(1+2^2+...+2^{2020}\right)⋮3\)
Vậy \(A⋮3\left(đpcm\right)\)
d) Ta có:
\(A=1+2+2^2+2^3+...+2^{2021}\)
\(A=1.\left(1+2+2^2\right)+2^3.\left(1+2+2^2\right)+...+2^{2019}.\left(1+2+2^2\right)\)
\(A=1.7+2^3.7+...+2^{2019}.7\)
\(A=7.\left(1+2^3+...+2^{2019}\right)⋮7\)
Vậy \(A⋮7\left(đpcm\right)\)
Chúc bạn học tốt!
19 tháng 5 2018
Bài 1: Bài giải
Vì a lẻ => a^2 lẻ => a^ - 1 chẵn
=> M chia hết cho 2
Vì a không chia hết cho 3=> a^2 chia hết cho 3 dư 1
=> a^2 - 1 chia hết cho 3=> M chia hết cho 3
Vì( 2,3 ) =1 => M chia hết cho 2.3=6
=> Mchia hết cho 6 (Đpcm)
Bài 2: 20. (x+1)^2 + (y - 3) ^2 =64
Vì 20.( x+1 )^2 \(\ge\)0 , ( y - 3 )^2\(\ge\)0
=> 20 . ( x+1 ) ^2 \(\le\)64
=> (x+1 ) ^2 \(\le\)64/20 + 3,2
Vì (x+1 ) ^2 là số chính phương
\(\orbr{\begin{cases}\left(x+1\right)^2=0\\\left(x+1^2\right)=1\end{cases}}\)
TH1 (x+1)^2 =0 => (y - 3)^2 =64 = \(\left(\mp8^2\right)\)
=.> x= -1 \(\orbr{\begin{cases}y-3=8\Rightarrow y=11\\y-3=-8\Rightarrow y=-5\end{cases}}\)
TH2 (x+1)^2 = 1 \(\Rightarrow\)(y - 3)^2 =44 (vô lí)
Vậy (x,y )= (-1 , -11), (-1 , -5)
Chúc bạn học tốt
9 tháng 2 2017
1/ a) \(x^2-x-1⋮x-1\)
=>\(x.\left(x-1\right)-1⋮x-1\)
=>\(-1⋮x-1\)(vì x.(x-1)\(⋮\)x-1)
=>x-1\(\inƯ\left(-1\right)\)
Đến đay tự làm
b/c/d/e/ tương tự
13 tháng 11 2021
A=2+22+23+...+299+2100A=2+22+23+...+299+2100
⇒2A=22+23+24+...+2100+2101⇒2A=22+23+24+...+2100+2101
⇒A=2101−2⇒A=2101−2
B=3+32+33+...+399+3100B=3+32+33+...+399+3100
⇒3B=32+33+34+...+3100+3101⇒3B=32+33+34+...+3100+3101
⇒2B=3101−3⇒2B=3101−3
⇒B=3101−32
CM
7 tháng 7 2019
a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:
10 tháng 10 2021
4₁ A= 2 +2²³ +2 ² + + 220
a₁ A = 2₁ [1 + 2 +2²¹ +. +2¹2):2 Vay A chia hết choi
b₁ A = 2 + 2² +2²+ + 220 (2 +2²) + (2 ² + 2 9) + . + (219+220)
= 2₁ (1 + 2) + 2² (2+1). .. +2 19 (2+1) + = 2₁3 + 2³.3 + ..+ 219.3.
= (2+2 ³+ + 219) 3:3 Vậy A chia hết cho 3 A = 2 + 2 ² + 2³ + 2ª +. 20 + 2.9+ +2
2+2 ³ + 2² +2²4 + + 218 + 720 +2²³ +2²+ +218 +220 2. (2 +2²) + 2² (1+2²) +.. + 218 ( 1 +2²) = 2 5 +2²5 + + 218 5. 12 +2° + 2 ... +218 ) 5 : 5.
vậy A chia hết cho 5
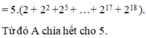
a) A = 2 + 22 + 23 + ... + 22000 (có 2000 số; 2000 chia hết cho 5)
A = (2 + 22 + 23 + 24 + 25) + (26 + 27 + 28 + 29 + 210) + ... + (21996 + 21997 + 21998 + 21999 + 22000)
A = 2.(1 + 2 + 22 + 23 + 24) + 26.(1 + 2 + 22 + 23 + 24) + ... + 21996.(1 + 2 + 22 + 23 + 24)
A = 2.31 + 26.31 + ... + 21996.31
A = 31.(2 + 26 + ... + 21996) chia hết cho 31 (đpcm)
b) A = 2 + 22 + 23 + ... + 22000
2A = 22 + 23 + 24 + ... + 22001
2A - A = (22 + 23 + 24 + ... + 22001) - (2 + 22 + 23 + ... + 22000)
A = 22001 - 2
c) 22x-1 - 2 = A
=> 22x-1 - 2 = 22001 - 2
=> 2x - 1 = 2001
=> 2x = 2001 + 1 = 2002
=> x = 2002 : 2 = 1001
Vậy x = 1001
a) A = 2 + 22 + 23 + ... + 22000 (có 2000 số; 2000 chia hết cho 5)
A = (2 + 22 + 23 + 24 + 25) + (26 + 27 + 28 + 29 + 210) + ... + (21996 + 21997 + 21998 + 21999 + 22000)
A = 2.(1 + 2 + 22 + 23 + 24) + 26.(1 + 2 + 22 + 23 + 24) + ... + 21996.(1 + 2 + 22 + 23 + 24)
A = 2.31 + 26.31 + ... + 21996.31
A = 31.(2 + 26 + ... + 21996) chia hết cho 31 (đpcm)