Cho ΔMNP vuông tại M, N=600 , vẽ phân giác NI (I thuộc MP) kẻ IK vuông NP.
a/ Chứng minh MI=IK.
b/ Chứng minh △MNK đều.
c/ Cho MN=12cm. Tính NP.
mọi người giúp em với 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
9 tháng 5 2023
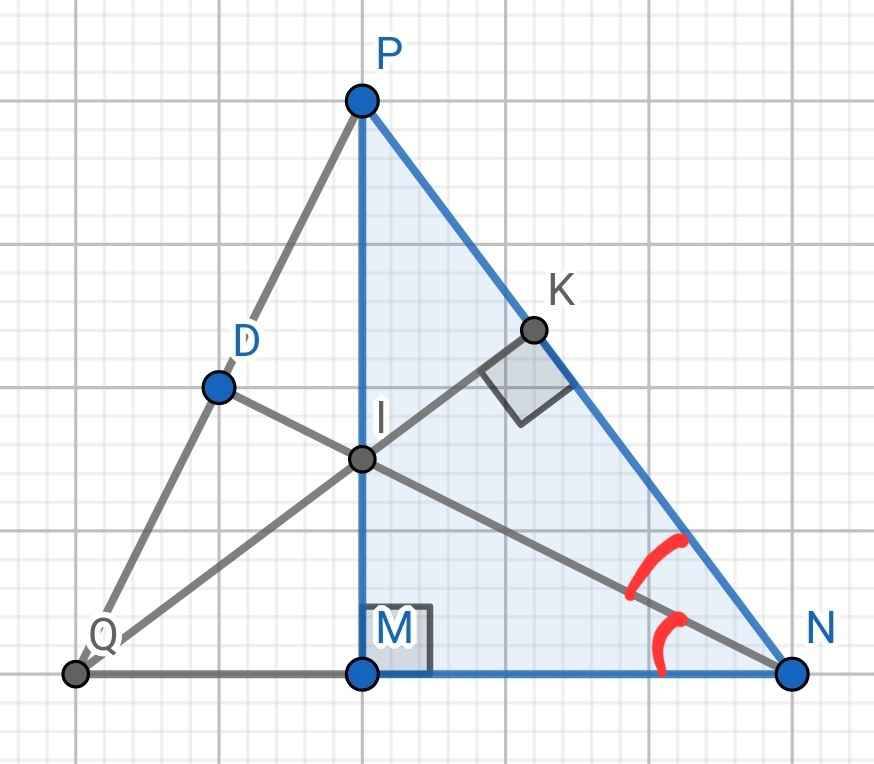
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
LA
4 tháng 3 2018
a) Áp dụng định lí pi-ta-go vào \(\Delta MNK\)vuông tại M có:
\(NK^2=NM^2+MK^2\Rightarrow NK^2=9^2+12^2\Rightarrow NK=15\)
b) Xét \(\Delta NMK\)vuông tại M và \(\Delta IMK\)vuông tại M có:
MK chung
NM=IM (gt)
\(\Rightarrow\Delta MNK=\Delta IMK\left(cgv-cgv\right)\)
\(\Rightarrow\widehat{NKM}=\widehat{IKM}\)hay \(\widehat{AKM}=\widehat{BKM}\)
Xét \(\Delta MAK\)vuông tại A và \(\Delta MBK\)vuông tại B có:
\(\widehat{AKM}=\widehat{BKM}\)(c/m trên)
MK chung
\(\Rightarrow\Delta MAK=\Delta MBK\left(ch-gn\right)\)
c) Vì \(\Delta MAK=\Delta MBK\)
\(\Rightarrow AK=BK\Rightarrow\Delta ABK\)cân tại K
\(\Rightarrow\widehat{KAB}=\widehat{KBA}\)
Áp dụng tính chất tổng 3 góc trong 1 tam giác có:
\(\widehat{KAB}+\widehat{KBA}+\widehat{NKI}=180^o\)
\(\Rightarrow\widehat{KAB}=\frac{180^o-\widehat{NKI}}{2}\left(1\right)\)
tới đây bn tự làm tiếp
10 tháng 5 2023
a: Xét ΔHNM vuông tại H và ΔMNP vuông tại M có
góc N chung
=>ΔHMN đồng dạng vói ΔMNP
b: \(NP=\sqrt{9^2+12^2}=15\left(cm\right)\)
MH=9*12/15=108/15=7,2cm
HP=12^2/15=9,6cm
S MHP=1/2*9,6*7,2=34,56cm2
14 tháng 2 2022
1: Xét ΔNMI vuông tại M và ΔNKI vuông tại K có
NI chung
\(\widehat{MNI}=\widehat{KNI}\)
Do đó: ΔNMI=ΔNKI
Suy ra: NM=NK
hay ΔNMK cân tại N
2: Xét ΔMIQ vuông tại M và ΔKIP vuông tại K có
IM=IK
\(\widehat{MIQ}=\widehat{KIP}\)
Do đó: ΔMIQ=ΔKIP
Suy ra: MQ=KP
Ta có: NM+MQ=NQ
NK+KP=NP
mà NM=NK
và MQ=KP
nên NQ=NP
hayΔNQP cân tại N
3: Xét ΔNQP có
NM/MQ=NK/KP
nên MK//QP
W
31 tháng 3 2020
a) Xét tam giác PNK vuông tại P và tam giác INK vuông tại I có:
\(\widehat{N}=\widehat{K}\)(tam giác MNK là tam giác cân)
NK:chung
Suy ra \(\Delta PNK=\Delta INK\)(cạnh huyền-góc nhọn)
=>PN=IK(1)
Mà do MNK cân tại M nên MN=MK(2)
Từ (1) và (2), suy ra MI=MP
b)Từ a) ta suy ra: \(\widehat{HNK}=\widehat{HKN}\)(hai góc tương ứng)<=> \(\widehat{IKH}=\widehat{PNH}\)
Xét tam giác PHN vuông tại P và tam giác IHK vuông tại I có:
\(NP=IK\left(cmt\right)\)
\(\widehat{IKH}=\widehat{PNH}\)(cmt)
Suy ra:....(cạnh góc vuông-góc nhọn kề)
=>HP=HI
Xét tam giác PMH và tam giác HMI có:
MH:chung
MP=MI(cmt)
HP=HI(cmt)
Suy ra:....(c-c-c)
=> \(\widehat{PMH}=\widehat{IMH}\)(hai góc tương ứng )
=>MH là tia phân giác của góc M
c) Từ b) suy ra MP=MI(2 cạnh tương ứng)
=>PMI là tam giác cân
Xét tam giác PMI có:
\(\widehat{P}=\widehat{I}=\frac{180^o-\widehat{M}}{2}\left(1\right)\)
Xét tam giác MNK có:
\(\widehat{K}=\widehat{N}=\frac{180^o-\widehat{M}}{2}\left(2\right)\)
=>\(\widehat{K}=\widehat{N}=\widehat{P}=\widehat{I}\)
Mà các cặp góc này ở vị trí đồng vị nên PI//NK
14 tháng 2 2022
1: Xét ΔNMI vuông tại M và ΔNKI vuông tại K có
NI chung
\(\widehat{MNI}=\widehat{KNI}\)
Do đó: ΔNMI=ΔNKI
Suy ra: NM=NK
hay ΔNMK cân tại N
2: Xét ΔMIQ vuông tại M và ΔKIP vuông tại K có
IM=IK
\(\widehat{MIQ}=\widehat{KIP}\)
Do đó: ΔMIQ=ΔKIP
Suy ra: MQ=KP
Ta có: NM+MQ=NQ
NK+KP=NP
mà NM=NK
và MQ=KP
nên NQ=NP
hayΔNQP cân tại N
3: Xét ΔNQP có
NM/MQ=NK/KP
nên MK//QP
11 tháng 7 2023
a: Xét ΔMIN vuông tại I và ΔMIP vuông tại I có
MN=MP
MI chung
=>ΔMIN=ΔMIP
b: Xét ΔMEI vuông tại E và ΔMFI vuông tại F có
MI chung
góc EMI=góc FMI
=>ΔMEI=ΔMFI
=>ME=MF
IN=IP=6/2=3cm
=>MI=4cm
8 tháng 3 2022
a: NK=15cm
b: Xét ΔKNI cso
KM là đường cao
KM là đường trung tuyến
DO đó: ΔKNI cân tại K
c: Xét ΔMAK vuông tại A và ΔMBK vuông tại B có
MK chung
\(\widehat{AKM}=\widehat{BKM}\)
Do đó: ΔMAK=ΔMBK
d: Xét ΔKIN có KB/KI=KA/KN
nên AB//IN
a) xét △KNI ⊥ tại K và △MNI ⊥ tại M có:
∠N1 = ∠N2 ( NI là đường phân giác của △MNP )
NI là cạnh chung
⇒ △KNI = △MNI ( cạnh huyền - góc nhọn )
⇒ KI = MI ( 2 cạnh bằng nhau )
b,c) Xin lỗi bạn mình ko biết . mình quên mất kiến thức rồi
có gì thì để bạn khác rả lời nhé❗ 3❤❤❤❤