Cho tam giác ABC. Lấy M,N làn lượt trên AB và AC sao cho AM = 1/2 AB, AN = 1/3 AC. Tính diện tích hình tam giác AMN biết diện tích hình tam giác ABC là 27cm2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

LH
8 tháng 6 2021
Câu:1 Vì AM=MB , AN=NC
Nên diện tích tam giác AMN=2ABC
=> Diện tích tam gác AMN = 180:2 = 90

13 tháng 2 2016
Bạn ơi, phải là AM = MB, AN = NC thì mình mới làm được, nếu AM = AB , AN = AC thì cùng một điểm có hai tên gọi và diện tích hình tam giác AMN bằng diện tích hình tam giác ABC. Khi nào đổi đề báo cho mình, mình giải cho

17 tháng 2 2023
Kẻ MK//BC
=>AM/MB=AK/KC=2
=>AK=2KC
=>AK=2/3AC
mà AN=1/2AC
nên AK/AN=4/3
=>AN/AK=3/4
=>\(S_{ANM}=\dfrac{3}{4}\cdot S_{AMK}\)
=>\(S_{AMK}=108\left(cm^2\right)\)
ΔABC có MK//BC
nên ΔAMK đồng dạng vơi ΔABC
=>\(\dfrac{S_{AMK}}{S_{ABC}}=\left(\dfrac{AM}{AB}\right)^2=\left(\dfrac{2}{3}\right)^2=\dfrac{4}{9}\)
=>\(S_{ABC}=108:\dfrac{4}{9}=27\cdot9=243\left(cm^2\right)\)
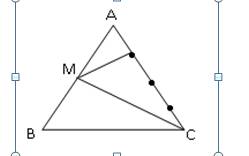
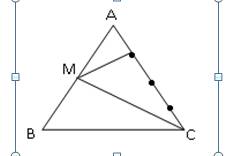
\(AM=\dfrac{1}{2}AB\)
=>\(S_{AMC}=\dfrac{1}{2}\cdot S_{ABC}=\dfrac{1}{2}\cdot27=13,5\left(cm^2\right)\)
Vì \(AN=\dfrac{1}{3}AC\)
nên \(S_{AMN}=\dfrac{1}{3}\cdot S_{AMC}=\dfrac{1}{3}\cdot13,5=4,5\left(cm^2\right)\)