Phân tích đa thức thành nhân tử: a3 +b3 +c3 -3abc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
NH
1
5 tháng 10 2021
a(b3 - c3) + b(c3 - a3) + c(a3 - b3)
= a(b3 - c3 ) + b( c3 - b3 + b3 - a3) + c(a3 - b3)
= a(b3 - c3) + b(c3 - b3) + b(b3 - a3) + c(a3 - b3)
= a(b3 - c3) - b(b3 - c3) - [b(a3 - b3) - c(a3- b3)]
= (b3 - c3)(a - b) - (a3- b3)(b - c)
= (b - c)(b2 + bc + c2)(a - b) - (a - b)(a2 + ab + b2)(b - c)
= (b - c)(a - b)(b2 + bc + c2 - a2 + ab - b2)
= (b - c)(a - b) [ (c2 - a2) + (bc - ab) ]
= (b - c)(a - b) [ (c - a)(c + a) + b(c - a) ]
= (b - c)(a -b) [ (c - a)(c + a + b) ]
= (a- b)(b - c)(c - a)(a + b + c)
CP
17 tháng 7 2021
a) \(x^4+2x^3-4x-4=\left(x^4+2x^3+x^2\right)-\left(x^2+4x+4\right)\)
\(=\left(x^2+x\right)^2-\left(x+2\right)^2=\left(x^2+x-x-2\right)\left(x^2+x+x+2\right)\)
\(=\left(x^2-2\right)\left(x^2+2x+2\right)\)
17 tháng 7 2021
a) Ta có: \(x^4+2x^3-4x-4\)
\(=\left(x^4+2x^3+x^2\right)-\left(x^2+4x+4\right)\)
\(=\left(x^2+x\right)^2-\left(x+2\right)^2\)
\(=\left(x^2+x-x-2\right)\left(x^2+x+x+2\right)\)
\(=\left(x^2-2\right)\cdot\left(x^2+2x+2\right)\)
WR
1
MH
26 tháng 10 2021
a(b3 - c3) + b(c3 - a3) + c(a3 - b3)
= a(b3 - c3 ) + b( c3 - b3 + b3 - a3) + c(a3 - b3)
= a(b3 - c3) + b(c3 - b3) + b(b3 - a3) + c(a3 - b3)
\(=\left[a\left(b^3-c^3\right)-b\left(b^3-c^3\right)\right]-\left[b\left(a^3-b^3\right)-c\left(a^3-b^3\right)\right]\)
= (b3 - c3)(a - b) - (a3- b3)(b - c)
= (b - c)(b2 + bc + c2)(a - b) - (a - b)(a2 + ab + b2)(b - c)
= (b - c)(a - b)(b2 + bc + c2 - a2 + ab - b2)
= (b - c)(a - b) [ (c2 - a2) + (bc - ab) ]
= (b - c)(a - b) [ (c - a)(c + a) + b(c - a) ]
= (b - c)(a -b) [ (c - a)(c + a + b) ]
= (a- b)(b - c)(c - a)(a + b + c)
A
1
24 tháng 4 2019
a3 ( c - b2 ) + b3 ( a - c2 ) + c3 ( b - a2 ) + abc ( abc - 1 )
= a3c - a3b2 + b3a - b3c2 + c3b - c3a2 + a2b2c2 - abc
= a2b2c2 - b3c2 - ( a2c3 - bc3 ) - ( a3b2 - ab3 ) + ( a3c - abc )
= b2c2 . ( a2 - b ) - c3 ( a2 - b ) - ab2 ( a2 - b ) + ac ( a2 - b )
= ( a2 - b ) ( b2c2 - c3 - ab2 + ac )
= ( a2 - b ) ( b2 - c ) ( c2 - a )
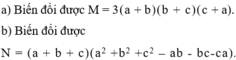
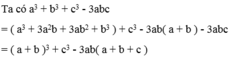
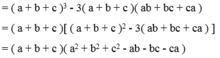
Ta có : \(a^3+b^3+c^3-3abc=\left(a+b\right)^3+c^3-3a^2b-3ab^2-3abc\)
\(=\left(a+b+c\right)\text{[}\left(a+b\right)^2-\left(a+b\right).c+c^2\text{ }\text{]}-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ac-bc+2ab-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)\)