Cho hình chóp S.ABCD, đáy ABCD là hình vuông; SA\(\perp\)(ABCD).a, Chứng minh các \(\Delta SBC,SDC\) là các \(\Delta\) vuông.b, Từ A kẻ AH\(\perp\)SB, AK\(\perp\)SC, AI\(\perp\)SD. Chứng minh 3 đường thẳng AH, AK, AI đồng phẳng.c, Chứng minh HI\(\perp\)AKd, Biết \(AB=a,SA=a\sqrt{2}\). Tính \(S_{AHKI}\) theo...
Đọc tiếp
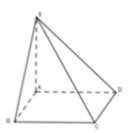
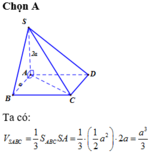
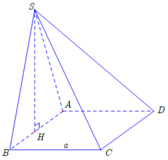
Cho hình chóp S.ABCD, đáy ABCD là hình vuông; SA\(\perp\)(ABCD).
a, Chứng minh các \(\Delta SBC,SDC\) là các \(\Delta\) vuông.
b, Từ A kẻ AH\(\perp\)SB, AK\(\perp\)SC, AI\(\perp\)SD. Chứng minh 3 đường thẳng AH, AK, AI đồng phẳng.
c, Chứng minh HI\(\perp\)AK
d, Biết \(AB=a,SA=a\sqrt{2}\). Tính \(S_{AHKI}\) theo a
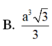
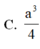
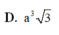
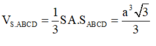
a: BC\(\perp\)BA(ABCD là hình vuông)
BC\(\perp\)SA(SA\(\perp\)(ABCD))
BA,SA cùng thuộc mp(SAB)
Do đó: BC\(\perp\)(SAB)
=>BC\(\perp\)SB
=>ΔSBC vuông tại B
Ta có: CD\(\perp\)AD(ABCD là hình vuông)
CD\(\perp\)SA(SA\(\perp\)(ABCD))
SA,AD cùng thuộc mp(SAD)
Do đó: CD\(\perp\)(SAD)
=>CD\(\perp\)SD
=>ΔSDC vuông tại D
b: Ta có: AH\(\perp\)SB
AH\(\perp\)BC(BC\(\perp\)(SAB))
SB,BC cùng thuộc mp(SBC)
Do đó: AH\(\perp\)(SBC)
=>AH\(\perp\)SC
CD\(\perp\)(SAD)
AI\(\subset\)(SAD)
Do đó: CD\(\perp\)AI
mà AI\(\perp\)SD
và SD,CD cùng thuộc mp(CSD)
nên AI\(\perp\)(SCD)
=>AI\(\perp\)SC
Ta có: AI\(\perp\)SC
AK\(\perp\)SC
AH\(\perp\)SC
=>AI,AK,AH đồng phẳng
c: Xét ΔSAB vuông tại A và ΔSAD vuông tại A có
SA chung
AB=AD
Do đó: ΔSAB=ΔSAD
=>\(\widehat{BSA}=\widehat{DSA}\); SB=SD
Xét ΔSHA vuông tại H và ΔSIA vuông tại I có
SA chung
\(\widehat{HSA}=\widehat{ISA}\)
Do đó: ΔSHA=ΔSIA
=>SH=SI
Xét ΔSBD có \(\dfrac{SH}{SB}=\dfrac{SI}{SD}\)
nên HI//BD
BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
AC,SA cùng thuộc mp(SAC)
Do đó:BD\(\perp\)(SAC)
mà HI//BD
nên HI\(\perp\)(SAC)
mà AK\(\subset\)(SAC)
nên HI\(\perp\)AK