mọi người giúp mình với ạ cảm ơn nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: BA=BE
DA=DE
=>BD là trung trực của AE
c: DA=DE
DE<DC
=>DA<DC
4:
a: ΔABC cân tại A có AI là phân giác
nên AI vuông góc BC tại I
b: Xét ΔABC có
CM,AI là trung tuyến
CM cắt AI tại G
=>G là trọng tâm
=>BG là trung tuyến của ΔABC
c: BI=CI=9cm
=>AI=căn 15^2-9^2=12cm
=>GI=1/3*12=4cm

Đổi 100ml = 0,1 lít
Ta có: \(n_{HCl}=2.0,1=0,2\left(mol\right)\)
a. PTHH: \(AgNO_3+HCl--->AgCl\downarrow+HNO_3\)
Theo PT: \(n_{AgNO_3}=n_{HCl}=0,2\left(mol\right)\)
Đổi 200ml = 0,2 lít
=> \(C_{M_{AgNO_3}}=\dfrac{0,2}{0,2}=1M\)
b. Ta có: \(m_{dd_{HNO_3}}=0,1\left(lít\right)\)
Theo PT: \(n_{HNO_3}=n_{HCl}=0,2\left(mol\right)\)
=> \(C_{M_{HNO_3}}=\dfrac{0,2}{0,1}=2M\)


a, Vì ABCD là hbh nên AB//CD
Do đó \(\widehat{A}+\widehat{D}=180^0\Rightarrow3\widehat{D}=180^0\Rightarrow\widehat{D}=60^0\Rightarrow\widehat{A}=120^0\)
Mà ABCD là hbh nên \(\left\{{}\begin{matrix}\widehat{A}=\widehat{C}=120^0\\\widehat{D}=\widehat{B}=60^0\end{matrix}\right.\)
b, Vì CE=CB nên tam giác CEB cân tại C
Do đó \(\widehat{B}=\widehat{CEB}\)
\(\Rightarrow\widehat{D}=\widehat{CEB}\left(1\right)\)
Mà ABCD là hbh nên AB//CD hay AE//CD
Do đó AECD là hình thang
Kết hợp (1) ta được AECD là hthang cân



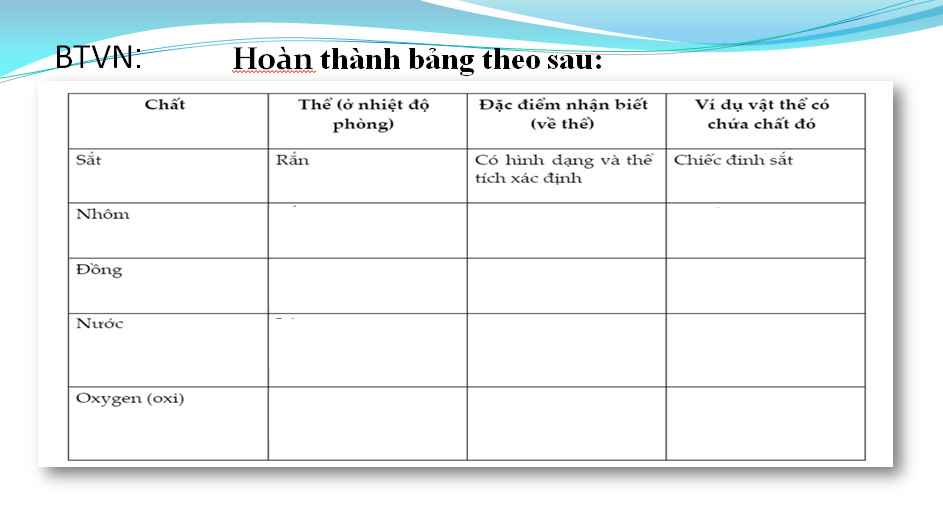

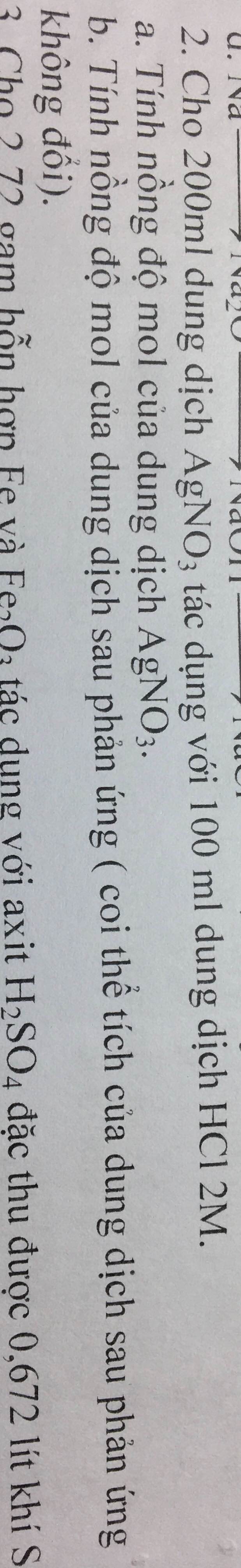
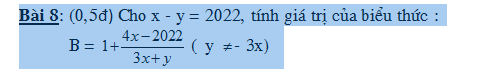 mọi người giúp mình với ạ, mai mình đi thi thi. Cảm ơn mọi người nhiều
mọi người giúp mình với ạ, mai mình đi thi thi. Cảm ơn mọi người nhiều 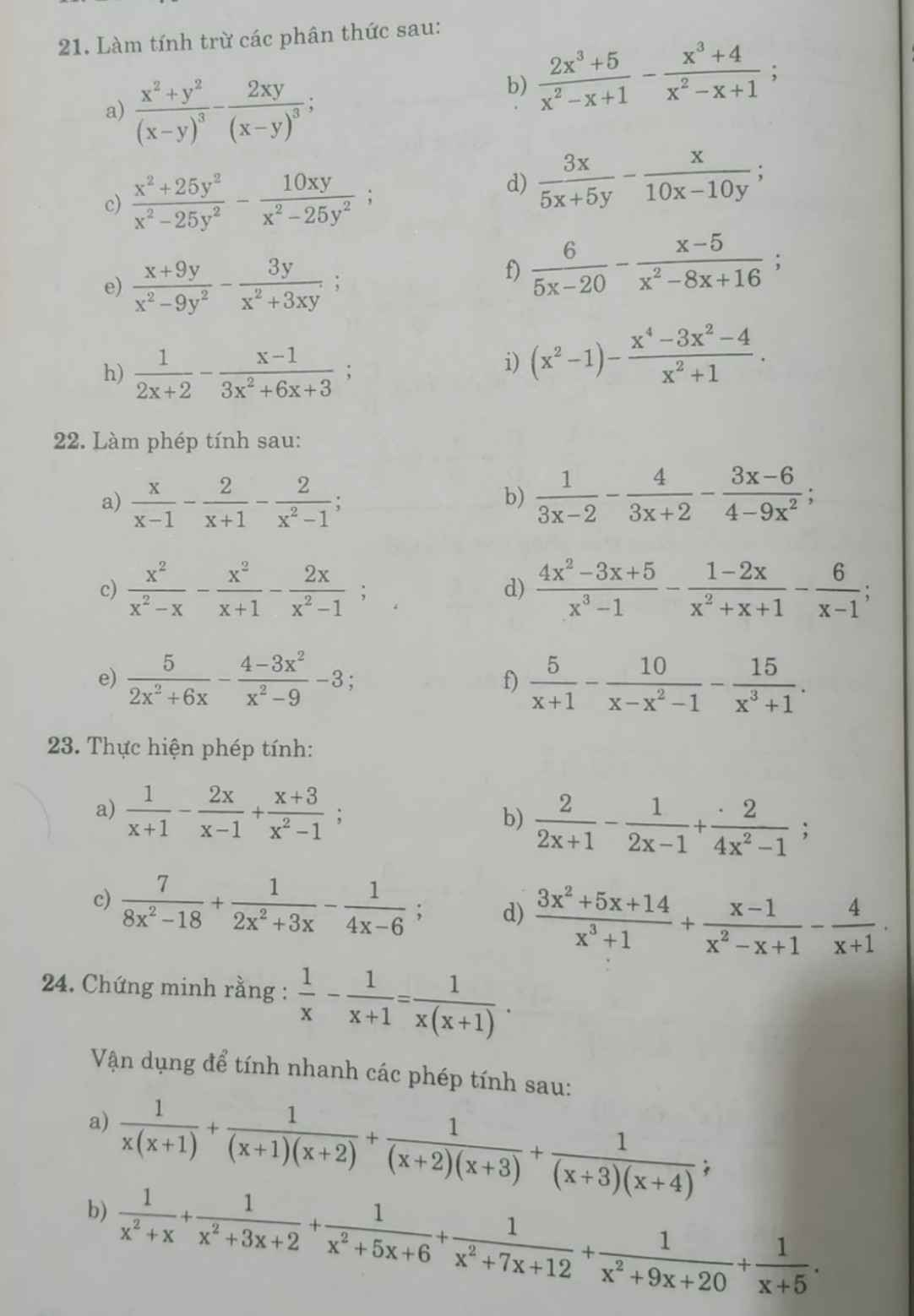

Bài 7:
a: Sửa đề: Tính góc ABD
Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
=>\(\widehat{MAC}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Ta có: AC//BD
AC\(\perp\)AB
Do đó: BD\(\perp\)AB
=>\(\widehat{ABD}=90^0\)
b: Ta có: ΔMAC=ΔMDB
=>AC=BD
Xét ΔBAC vuông tại A và ΔABD vuông tại B có
AB chung
AC=BD
Do đó: ΔBAC=ΔABD
c: Ta có: ΔBAC=ΔABD
=>BC=AD
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}BC\)
Bài 8:
a: ta có: BC=BD
B nằm giữa D và C(BD và BC là hai tia đối nhau)
Do đó: B là trung điểm của DC
AB và AE là hai tia đối nhau
=>A nằm giữa B và E
=>\(BE=BA+AE=2AB+AB=3AB\)
=>\(\dfrac{EA}{EB}=\dfrac{2AB}{3AB}=\dfrac{2}{3}\)
Xét ΔEDC có
EB là đường trung tuyến
\(EA=\dfrac{2}{3}EB\)
Do đó: A là trọng tâm của ΔEDC
b: Xét ΔEDC có
A là trọng tâm
nên CA đi qua trung điểm của DE