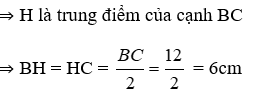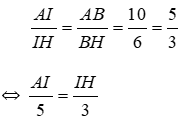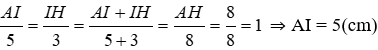Cho tam giác ABC cân tại A. AB=10cm, BC=12cm. I là giao điểm của các đường phân giác. Tính AI.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:

Tam giác ABC cân tại A nên đường phân giác AH đồng thời là đường trung trực của BC
Áp dụng định lý pitago ta được:
\(AH^2=AB^2-BH^2=10^2-6^264\Rightarrow AH=8\)
Áp dụng tính chất đường phân giác ta được:

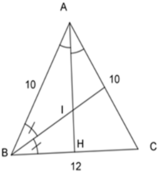
Ta có: AB = AC = 10cm
Suy ra ΔABC cân tại A
Có I là giao các đường phân giác của ΔABC
Suy ra AI, BI là đường phân giác của ΔABC
Gọi H là giao của AI và BC
Khi đó ta có AH vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân ABC (tính chất tam giác cân).
=> H là trung điểm của cạnh BC
=> BH = HC = B C 2 = 12 2 = 6cm
Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:
A H 2 + B H 2 = A B 2 ⇔ A H 2 + 6 2 = 10 2 ⇔ A H 2 = 100 – 36 = 64 ⇒ A H = 8
Vì BI là phân giác của tam giác ABH nên: A I I H = A B B H = 10 6 = 5 3
⇔ A I 5 = I H 3
Theo tính chất dãy tỉ số bằng nhau ta có:
A I 5 = I H 3 = A I + I H 5 + 3 = A H 8 = 8 8 = 1
=> AI = 5(cm)
Đáp án: C

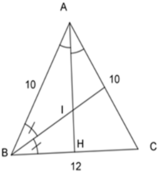
Ta có: AB = AC = 10cm
Suy ra ΔABC cân tại A
Có I là giao các đường phân giác của ΔABC
Suy ra AI, BI là đường phân giác của ΔABC
Gọi H là giao của AI và BC
Khi đó ta có AH vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân ABC (tính chất tam giác cân).
=> H là trung điểm của cạnh BC
=> BH = HC = B C 2 = 12 2 = 6cm
Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:
A H 2 + B H 2 = A B 2 ⇔ A H 2 + 6 2 = 10 2 ⇔ A H 2 = 100 – 36 = 64 ⇒ A H = 8
Vì BI là phân giác của tam giác ABH nên: A B B H = A I I H = A H − I H I H
ó 10 6 = 8 − I H I H ó 10IH = 48 – 6IH ó IH = 3
Áp dụng định lý Pitago trong tam giác BHI vuông tại H, ta có:
B I 2 = I H 2 + B H 2 ⇔ B I 2 = 3 2 + 6 2 ⇔ B I 2 = 45 ⇒ B I = 3 5
Đáp án: D

TK
Ta có: AB = AC = 10cm
Suy ra ΔABC cân tại A
Có I là giao các đường phân giác của ΔABC
Suy ra AI, BI là đường phân giác của ΔABC
Gọi H là giao của AI và BC
Khi đó ta có AH vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân ABC (tính chất tam giác cân).
Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:
AH2 + BH2 = AB2
⇔ AH2 + 62 = 102
⇔ AH2 = 100 – 36 = 64
⇒ AH = 8
Vì BI là phân giác của tam giác ABH nên:
Theo tính chất dãy tỉ số bằng nhau ta có:
Đáp án cần chọn là: C

a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là trung tuyến
nên AM là đường cao
BC=12cm nên BM=6cm
=>AM=8(cm)
c: I cách đều ba cạnh nên I là giao điểm của ba đường phân giác
=>AI là phân giác của góc BAC
mà AM là phân giác của góc BC
nên A,I,M thẳng hàng
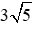 cm
cm