Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xóa chữ số \(0\)ở tận cùng bên phải đi ta được số mới giảm đi \(10\)lần so với số ban đầu.
Số bé là \(1\)phần thì số lớn là \(10\)phần.
Số bé là:
\(1089\div\left(1+10\right)\times1=99\)
Số lớn là:
\(99\times10=990\)

1/ Đề đúng phải là \(3x^2+2y^2\) có giá trị nhỏ nhất nhé.
Áp dụng BĐT BCS , ta có
\(1=\left(\sqrt{2}.\sqrt{2}x+\sqrt{3}.\sqrt{3}y\right)^2\le\left[\left(\sqrt{2}\right)^2+\left(\sqrt{3}\right)^2\right]\left(2x^2+3y^2\right)\)
\(\Rightarrow2x^2+3y^2\ge\frac{1}{5}\). Dấu "=" xảy ra khi \(\begin{cases}\frac{\sqrt{2}x}{\sqrt{2}}=\frac{\sqrt{3}y}{\sqrt{3}}\\2x+3y=1\end{cases}\) \(\Leftrightarrow x=y=\frac{1}{5}\)
Vậy \(3x^2+2y^2\) có giá trị nhỏ nhất bằng 1/5 khi x = y = 1/5
2/ Áp dụng bđt AM-GM dạng mẫu số ta được
\(6=\frac{\left(\sqrt{2}\right)^2}{x}+\frac{\left(\sqrt{3}\right)^2}{y}\ge\frac{\left(\sqrt{2}+\sqrt{3}\right)^2}{x+y}\)
\(\Rightarrow x+y\ge\frac{\left(\sqrt{2}+\sqrt{3}\right)^2}{6}\)
Dấu "=" xảy ra khi \(\begin{cases}\frac{\sqrt{2}}{x}=\frac{\sqrt{3}}{y}\\\frac{2}{x}+\frac{3}{y}=6\end{cases}\) \(\Rightarrow\begin{cases}x=\frac{2+\sqrt{6}}{6}\\y=\frac{3+\sqrt{6}}{6}\end{cases}\)
Vậy ......................................

Số lớn nhất được lập bởi năm chữ số 9,0,6,1,5 trong đó mỗi chữ số chỉ được viết đúng một lần là 96510

Ta có \(\sqrt{8a^2+56}=\sqrt{8\left(a^2+7\right)}=2\sqrt{2\left(a^2+ab+2bc+2ca\right)}\)
\(=2\sqrt{2\left(a+b\right)\left(a+2c\right)}\le2\left(a+b\right)+\left(a+2c\right)=3a+2b+2c\)
Tương tự \(\sqrt{8b^2+56}\le2a+3b+2c;\)\(\sqrt{4c^2+7}=\sqrt{\left(a+2c\right)\left(b+2c\right)}\le\frac{a+b+4c}{2}\)
Do vậy \(Q\ge\frac{11a+11b+12c}{3a+2b+2c+2a+3b+2c+\frac{a+b+4c}{2}}=2\)
Dấu "=" xảy ra khi và chỉ khi \(\left(a,b,c\right)=\left(1;1;\frac{3}{2}\right)\)
a) \(P=1957\)
b) \(S=19.\)
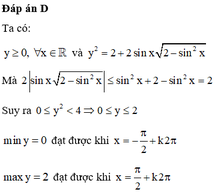
Là 1000 nha
1000 bạn nha