Tam giác ABC, B(1;2) phân giác trong của góc A có pt là 2x+y-1=0, khoảng cách từ C đến phân giác đó gấp 3 lần khoảng cách từ B đến phân giác đó, C thuộc trục tung. Tìm các đỉnh còn lại của tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
b: Vì AB<AC<BC
nên góc C<góc B<góc A

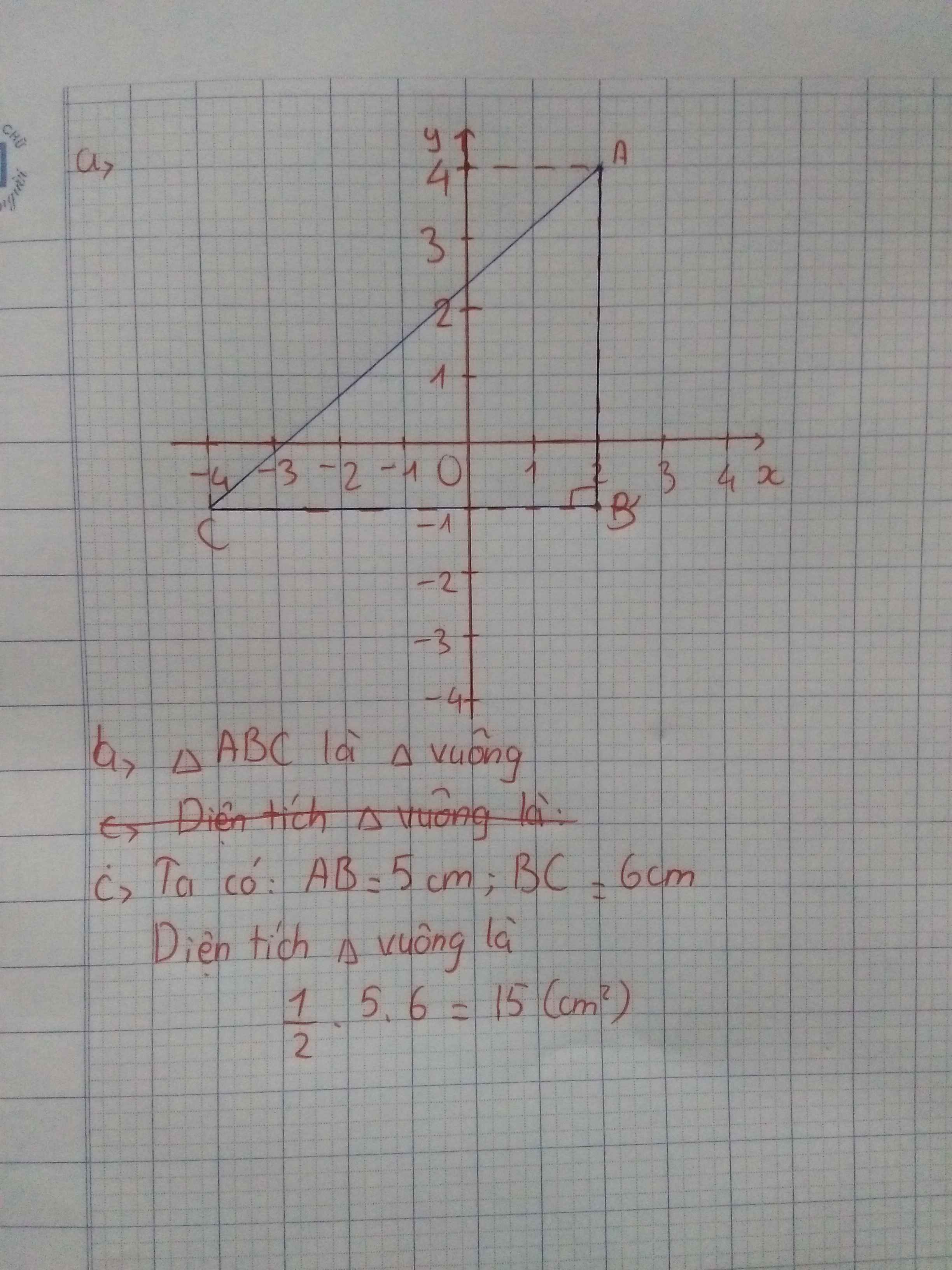
b) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(2-2\right)^2+\left(4+1\right)^2}=5\)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(2+4\right)^2+\left(4+1\right)^2}=\sqrt{61}\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(2+4\right)^2+\left(-1+1\right)^2}=6\)
Ta có: \(BA^2+BC^2=5^2+6^2=25+36=61\)
\(AC^2=\left(\sqrt{61}\right)^2=61\)
Do đó: \(AC^2=BA^2+BC^2\)(=61)
Xét ΔABC có \(AC^2=BA^2+BC^2\)(cmt)
nên ΔABC vuông tại B(Định lí Pytago đảo)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{BA\cdot BC}{2}=\dfrac{5\cdot6}{2}=\dfrac{30}{2}=15\left(cm^2\right)\)

Tọa độ điểm C:
\(\left\{{}\begin{matrix}x_C=3x_I-x_A-x_B=1\\y_C=3y_I-y_A-y_B=-4\end{matrix}\right.\Rightarrow C\left(1;-4\right)\)
Ta có:
\(\overrightarrow{AH}=\left(a-3;b+1\right)\)
\(\overrightarrow{BH}=\left(a+1;b-2\right)\)
\(\overrightarrow{BC}=\left(2;-6\right)\)
\(\overrightarrow{AC}=\left(-2;-3\right)\)
Theo giả thiết
\(AH\perp BC\Rightarrow2\left(a-3\right)-6\left(b+1\right)=0\Leftrightarrow a-3b=6\left(1\right)\)
\(BH\perp AC\Rightarrow-2\left(a+1\right)-3\left(b-2\right)=0\Leftrightarrow2a+3b=4\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=\dfrac{10}{3}\\b=-\dfrac{8}{9}\end{matrix}\right.\Rightarrow a+3b=\dfrac{2}{3}\)

Lời giải:
$\widehat{A}+\widehat{B}+\widehat{C}=180^0$
$\Rightarrow \widehat{A}=180^0-\widehat{B}-\widehat{C}=180^0-45^0-45^0=90^0$
$\Rightarrow$ tam giác $ABC$ là tam giác vuông tại $A$. Mà $\widehat{B}=\widehat{C}$ nên $ABC$ là tam giác vuông cân ở A
\(\Delta:2x+y-1=0\)
Gọi \(C=\left(0;m\right)\) thuộc trục tung.
Ta có \(d\left(C;\Delta\right)=3d\left(B;\Delta\right)\)
\(\Leftrightarrow\dfrac{5\left|2.1+2.1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{\left|2.0+1.m-1\right|}{\sqrt{2^2+1^2}}\)
\(\Leftrightarrow\left|m+1\right|=15\)
\(\Leftrightarrow\left[{}\begin{matrix}m=14\\m=-16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}C=\left(0;14\right)\left(\text{loại do cùng phía với }\Delta\right)\\C=\left(0;-16\right)\end{matrix}\right.\)
\(\Rightarrow C=\left(0;-16\right)\)
Lấy B' đối xứng với B qua \(\Delta\), M là giao điểm của BB' và \(\Delta\)
BB' có phương trình: \(x-2y+3=0\)
M có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}2x+y-1=0\\x-2y+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{5}\\y=\dfrac{7}{5}\end{matrix}\right.\Rightarrow M=\left(-\dfrac{1}{5};\dfrac{7}{5}\right)\)
\(\Rightarrow B'=\left(-\dfrac{7}{5};\dfrac{4}{5}\right)\)
AC có phương trình \(\dfrac{x}{0+\dfrac{7}{5}}=\dfrac{y+16}{-16-\dfrac{4}{5}}\Leftrightarrow84x+7y+112=0\)
A có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}84x+7y+112=0\\2x+y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{17}{10}\\y=\dfrac{22}{5}\end{matrix}\right.\Rightarrow A\left(-\dfrac{17}{10};\dfrac{22}{5}\right)\)