Trên mặt phẳng tọa độ Oxy lấy 1 điểm \(M\left(x_M;y_M\right)\) di động sao cho \(x_M^2+y_M^2=k\)(với \(k\)là một hằng số và \(k>0\)). Tìm quỹ tích của điểm M.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tình cờ hay cố ý mà dữ liệu bài toán có rất nhiều sự trùng hợp dẫn đến lời giải rất dễ dàng:
\(M\in d_1\Rightarrow y_M=\left(m^2+1\right)x_M-2\Rightarrow y_M+2=\left(m^2+1\right)x_M\)
\(\Rightarrow A=2020\left(m^2+1\right)x_M^2\ge0\)
\(A_{min}=0\) khi \(m=0\)
Khi đó điểm M là \(M\left(0;-2\right)\)

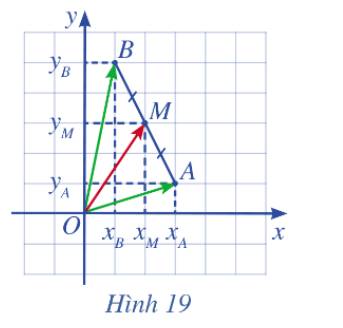
a) M là trung điểm của đoạn thẳng AB, áp dụng tính chất trung điểm ta có:
\(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) G là trọng tâm của tam giác ABC, áp dụng tính chất trọng tâm của tam giác ta có:
\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
c) Ta có \(\overrightarrow {OA} = \left( {{x_A};{y_A}} \right),\overrightarrow {OB} = \left( {{x_B};{y_B}} \right),\overrightarrow {OC} = \left( {{x_C};{y_C}} \right)\)
Suy ra:
\(\begin{array}{l}\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right)} \right]\\ = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\end{array}\)
\(\begin{array}{l}
\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left[ {\left( {{x_A};{y_A}} \right) + \left( {{x_B};{y_B}} \right) + \left( {{x_c};{y_c}} \right)} \right]\\
= \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)
\end{array}\)
Mà ta có tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ điểm M, nên ta có
Tọa độ điểm M là \(\left( {{x_M};{y_M}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm G là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)

a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

b) Xét tam giác OMB vuông tại O có:
BM2 = OM2 + OB2 = 1 + 1 = 2 ⇒ BM = √2
Tương tự tam giác OAB vuông tại O có:
B A 2 = O A 2 + O B 2 = 1 + 1 = 2 ⇒ BA = 2
Xét tam giác MAB có:
B M 2 + B A 2 = 2 + 2 = 4 = A M 2
⇒ ΔMAB vuông tại B
Do đó, khoảng cách từ M đến đường thẳng (d) là độ dài đoạn BM = 2

https://h.vn/hoi-dap/question/33566.html
Bạn vào đây xem nhé'
Học tốt!!!!!

Gọi\(M ′ ( x ; y ) . Suy ra −−→ I M = ( − 9 ; − 1 ) , −−→ I M ′ = ( x − 2 ; y − 3 ) .\)
Ta có V(I,−2)(M)=M′⇔−−→IM′=−2−−→IMV(I,−2)(M)=M′⇔IM′→=−2IM→ ⇒{x−2=−2.(−9)y−3=−2.(−1)⇒{x−2=−2.(−9)y−3=−2.(−1) ⇔{x=20y=5⇒M′(20;5)
hỉu ko ?
sai hay đúng vậy ?????????
T_T
mog đúng