3 duong cao cua tam giac ABC la 4;12;a .Biet a la 1 so tu nhien tim a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VM
23 tháng 9 2019
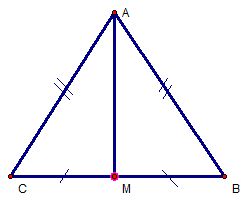
a) Xét 2 \(\Delta\) \(ABM\) và \(ACM\) có:
\(AB=AC\left(gt\right)\)
\(BM=CM\) (vì M là trung điểm của \(BC\))
Cạnh AM chung
=> \(\Delta ABM=\Delta ACM\left(c-c-c\right)\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng)
=> \(AM\) là đường phân giác của \(\widehat{A}.\)
b) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
Có \(AM\) là đường phân giác (cmt) đồng thời \(AM\) cũng là đường cao của \(\Delta ABC.\)
=> \(AM\) là đường cao của \(\Delta ABC.\)
c) Theo câu b) ta có \(\Delta ABC\) cân tại A.
Có \(AM\) là đường cao đồng thời \(AM\) cũng là đường trung trực của \(\Delta ABC.\)
=> \(AM\) là đường trung trực của \(BC.\)
Chúc bạn học tốt!
10 tháng 6 2019
Xét \(\Delta AMC\)và \(\Delta ABC\)có
Chung chiều cao hạ từ A xuống BC
\(MC=\frac{1}{4}BC\)
=>\(S_{AMC}=\frac{1}{4}S_{ABC}\)
Mặt khác \(\Delta AMC\)và \(\Delta ABC\)có chung đáy AC =>\(MH=\frac{1}{4}BK\)
VM
22 tháng 9 2019
Mình nghĩ đề bài phải là \(\Delta ABC\) cân tại A chứ. Hoàng Thùy Linh
7 tháng 9 2017
gtnn MB=MC = 3cm khi tg ABC vuông cân tại A , lúc đó đường cao AM =3cm
23 tháng 2 2023
a: Xét tư giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
Xét tứ giác CDHE có
góc CDH+góc CEH=180 độ
=>CDHE là tứ giác nội tiếp
b: CDHE là tứ giác nội tiếp
=>gó BED=góc FCB
góc FEH=góc BAD
mà góc FCB=góc BAD
nên góc BED=góc FEB
=>EB là phân giác của góc FED
c: góc IEO=góc IEH+góc OEH
=góc IHE+góc OBE
=góc BHD+góc CBH=90 độ
=>IE là tiếp tuyến của (O)
gọi a,b,c là độ dại 3 cạnh,ha,hb,hc là 3 đường cao tương ứng
ha = 4 và hb = 12,ta tìm hc
+ ta có
S = 1/2*a.ha
=>a = 2S/ha
tương tự
b = 2S/hb
và
c=2S/hc
+ do ABC la 1 tam giác nên
* a + b > c
=> 2S/ha + 2S/hb > 2S/hc
<> 1/hc < 1/4 + 1/12 = 1/3
=> hc > 3
* b + c > a
=> 1/12 + 1/hc > 1/4
<>1/hc > 1/6
=> hc < 6
do hc nguyên nên hc = 4 hoạc hc = 5
Thay a = x cho dễ
Ta có :
4a/2 = 12b/2 = xc/2 = S (S là diện tích tam giác)
=> a = 2 ; b = 6 ; c = 2S /x
Do x - y < z < x + y (bất đẳng thức trong tam giác)
=> S/2 - S/6 < 2S/x < S/2 + S/6
=> 2S /6 < 2S /x < 2S/3 . Mà x thuộc Z
=> x = {4 ,5}