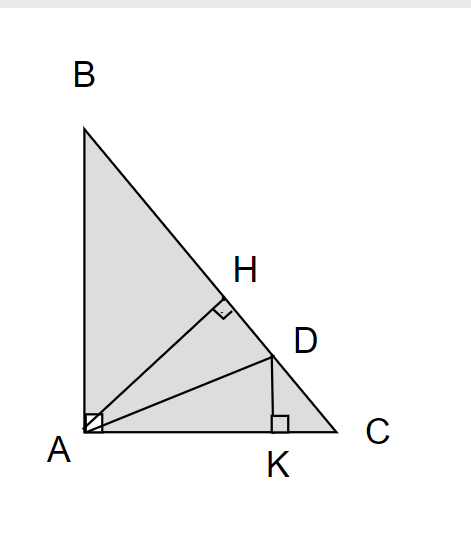
cho tam giác abc vuông tại a,có ab < ac. Trên cạnh BC lấy điểm D sao cho BD=BA.Kẻ AH vuông góc với bc,kẻ dk vuông góc với ac
a, chứng minh góc bad = góc bda
b, cm ad là phân giác của góc hac
c, cm ak=ah
d, cm ab+ac < BC+AH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 1 2022
a: \(BC=\sqrt{4^2+5^2}=\sqrt{41}\left(cm\right)\)
b: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
Suy ra: \(\widehat{BAD}=\widehat{BDA}\)
c: Ta có: \(\widehat{HAD}+\widehat{BDA}=90^0\)
\(\widehat{KAD}+\widehat{BAD}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên AD là tia phân giác của góc HAC
TM
8 tháng 5 2017
Do BD=BA => tam giác ABD cân tại B => góc BAD=góc BDA
Dễ thấy: góc BAC=góc DKC=90o mà chúng đồng vị => AB//KD => góc BAD=góc ADK (so le trong)
mà góc BAD=góc BDA => góc BDA=ADK hay góc HDA=góc ADK
Xét tam giác vuông AHD và tam giác vuông AKD có:AD chung;góc HDA=góc ADK (cmt)
=> tam giác vuông AHD = tam giác vuông AKD (cạnh huyền-góc nhọn)
=> góc HAD=góc KAD (2 góc tương ứng);AD=AK(2 cạnh tương ứng)
góc HAD=góc KAD => AD là phân giác góc HAK hay AD là phân giác góc HAC
LL
16 tháng 4 2019
a) Vì BD = BA nên ΔBAD cân tại B
=> BADˆgóc BAD = g BDA (góc đáy) →-> đpcm
b) Ta có: góc BAD + g DAC = 90o
=> g DAC = 90o - g BAD (1)
Áp dụng tc tam giác vuông ta có:
g HAD + g BDA = 90o
=> g HAD = 90o - g BDA (2)
mà góc BAD = g BDA (câu a)
=> gDAC = g HAD
=> AD là tia pg của g HAC.
c) Áp dụng tc tổng 3 góc trong 1 tg ta có:
g AHD + g HDA + g HAD = 180o
=> 90o + g HDA + g HAD = 180o
=> g HDA + g HAD = 90o (3)
g DAC + g DKA + g ADK = 180o
=> g DAC + 90o + g ADK = 180o
=> g DAC + g ADK = 90o (4)
mà gDAC = g HAD hay gDAK = gHAD
Xét tgHAD và tgKAD có:
g HDA = g ADK (c/m trên)
AD chung
g HAD = g DAK (c/m trên)
=> tgHAD = tgKAD (g.c.g)
=> AH = AK (2 cạnh t/ư)
Chú thích: tg: tam giác
g: góc.
16 tháng 4 2019
a, Vì BD = BA (gt) => ∆BAD là ∆ cân
=> góc BAD = góc BDA
b, Xét ∆ABC vuông tại A có
CAD + DAB = 90 độ
Xét ΔAND vuông tại N
DAN + ADN = 90 độ
Mà góc BAD = góc BDA (câu a) => góc CAD = góc DAN
=> AD là tia phân giác góc HAC
c, Xét Δ KAD và Δ HAD có :
Góc HDA = góc KDA = 90 độ (gt)
AD là cạnh huyền chung
góc KAD = góc DAN
=> ΔKAD = ΔCAN ( ch + gn)
=> AK = AH (2 cạnh tương ứng)
d,
AC + AB = CK + KA + AB
BC + AN = CB + DB + AN
AN = KA
AB = BD
CD > CK
=> BC + AN > AC + AB
22 tháng 6 2023
a: ΔBAD cân tại B
=>góc BAD=góc BDA
b: góc BAD+góc CAD=90 độ
góc BDA+góc HAD=90 độ
mà góc BAD=góc BDA
nên góc CAD=góc HAD
=>AD là phân giác của góc HAC
c: Xét ΔABC có AB<AC
nên góc ABC>góc ACB
d: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
góc HAD=góc KAD
=>ΔAHD=ΔAKD
=>AH=AK
e: (AB+AC)^2=AB^2+AC^2+2*AB*AC
=BC^2+2*AH*BC<BC^2+2*AH*BC+AH^2=(BC+AH)^2
=>AB+AC<BC+AH
11 tháng 5 2022
a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của góc HAC
YP
11 tháng 5 2022
c, Ta có: Góc CAD= góc HAD
hay góc KAD= góc HAD
Xét △ AHD và △AKD có:
AD chung
Góc AHD= góc AKD= 90 độ
Góc KAD= góc HAD
=> △AHD= △AKD (cạnh huyền- góc nhọn)
=> AH= AK (2 cạnh tương ứng)
15 tháng 3 2021
Cho tam giác ABC vuông tại A, có AB < AC. Trên cạnh BC lấy điểm D sao cho
BD = BA.
Kẻ AH vuông góc với BC, kẻ DK vuông góc với AC.
| a)Chứng minh : ; c) Chứng minh : AK = AH. | b)Chứng minh : AD là phân giác của góc HAC |
BAˆD = BDˆA