Cho ba điểm A B C , , theo thứ tự đó thuộc đường thẳng d , biết AB 4 cm AC 6 cm
B , Gọi D là trung điểm của đoạn thẳng AB. Hỏi B có là trung điểm của đoạn thẳng DC không? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LB
27 tháng 12 2016
Đoạn thẳng AQc là đoạn thẳng AC , đúng khống bạn ? Nếu đúng , bài giải sẽ như sau :
a) Trên tia AC , ta có AB < AC ( vì 4cm < 8cm ) , điểm B nằm giữa 2 điểm A và C nên :
AB + BC = AC
4 + BC = 8
BC = 8 - 4
BC = 4 ( cm )
Vậy , BC = 4 cm .
Ta có :
- Điểm A nằm giữa 2 điểm A và C
- AB = BC ( vì 4 cm = 4 cm )
Vậy điểm B là trung điểm của đoạn thẳng AC .
b) Trên tia AC , ta có AD < AB ( vì 3 cm < 4 cm ) , điểm D nằm giữa 2 điểm A và B nên :
AD + BD = AB
3 + BD = 4
BD = 4 - 3
BD = 1 ( cm )
Vậy , BD = 1 cm .
Bạn nào thấy mình đúng , nhớ k cho mình nha !
27 tháng 12 2016
Ta thay
Ab=4cm
Ac=8cm
Ab<Ac ( 4<8 )
Suy ra B nam giua Ac
Dc+bd=ab
Hay 3+bd=4
Bd=4-3=1
Suy ra Bd =1
8 tháng 4 2020
câu 9
a) ta có AB=6
=> AM=BM=3 cm
mà MC=AM-MC=3-2=1 cm
MD=MB-BD=3-2=1 cm
=> MC=MD
=> M là trung điểm của CD
b) C là trung điểm của AD
D là trung điểm của BC
8 tháng 4 2020
câu 10
a) AB + BO có giá trị nhỏ nhất khi và chỉ khi <=> O trùng B.
b) AB + BO = 2BO <=> AB = BO <=> O trùng A.
c) AB + BO = 3BO <=> AB = 2BO <=> O là trung điểm của AB.
Chúc bạn học tốt
CM
4 tháng 6 2018
a) Trên tia Ax có B, C và AB < AC (vì 4 cm < 8 cm ), nên B nằm giữa A và C.
b) B nằm giữa A và C nên : AB + BC = AC
4 + BC = 8
BC = 8 – 4 = 4 (cm)
Ta có B nằm giữa A và C và AB = BC = 4 cm nên B là trung điểm của đoạn thẳng AC
c) D là trung điểm của đoạn thẳng AB nên:
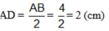
D là trung điểm của AB; B nằm giữa A và C nên D nằm giữa A và C
Do đó: AD + DC = AC
2 + DC = 8
DC = 8 – 2 = 6 (cm)
8 tháng 12 2017
Bạn tự vẽ hình ra nha
giải
a, Ta có : AC + CB = AB
=> CB = AB - AC
=> CB = 12 - 6 = 6 ( cm )
=> CB = AC = 6 ( cm )
=> Điểm C là trung điểm của đoạn thẳng AB
b, Ta có : M là trung điểm của AC
=> AM = MC = AC : 2 = 6 : 2 = 3 ( cm )
N là trung điểm của CB
=> CN = NB = CB : 2 = 6 : 2 = 3 ( cm )
=> MN = MC + CN = 3 + 3 = 6 ( cm )
14 tháng 12 2020
qqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqqq