Giúp mình với ạ (╥﹏╥)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 11 2021
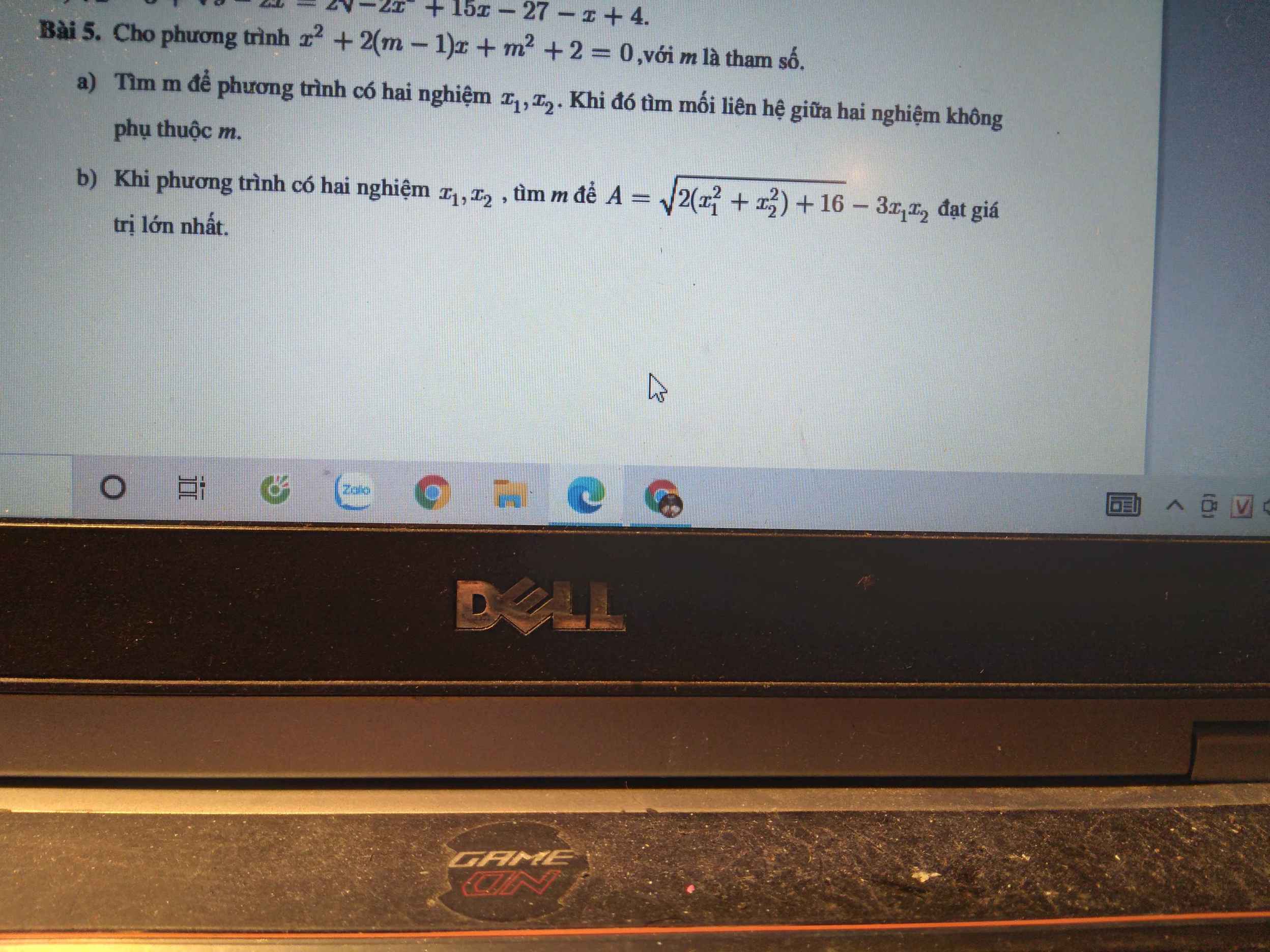
\(\Delta'=\left(m-1\right)^2-\left(m^2+2\right)=-2m-1\ge0\Rightarrow m\le-\dfrac{1}{2}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2+2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x_1+x_2+2}{2}=m\\x_1x_2-2=m^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(\dfrac{x_1+x_2+2}{x}\right)^2=m^2\\x_1x_2-2=m^2\end{matrix}\right.\)
\(\Rightarrow\left(\dfrac{x_1+x_2+2}{2}\right)^2=x_1x_2-2\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m
b.
\(A=\sqrt{2\left(x_1+x_2\right)^2-4x_1x_2+16}-3x_1x_2\)
\(=\sqrt{8\left(m-1\right)^2-4\left(m^2+2\right)+16}-3\left(m^2+2\right)\)
\(=\sqrt{4m^2-16m+16}-3\left(m^2+2\right)\)
\(=\sqrt{\left(4-2m\right)^2}-3m^2-6\)
\(=\left|4-2m\right|-3m^2-6\)
\(=4-2m-3m^2-6\) (do \(m\le-\dfrac{1}{2}\Rightarrow4-2m>0\))
\(=-3m^2-2m-2\)
\(=-\dfrac{1}{4}\left(12m^2+8m+1\right)-\dfrac{7}{4}\)
\(=-\dfrac{1}{4}\left(6m+1\right)\left(2m+1\right)-\dfrac{7}{4}\le-\dfrac{7}{4}\)
\(A_{max}=-\dfrac{7}{4}\) khi \(m=-\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2022
Bài 1:
Do d đi qua A nên phương trình d có dạng:
\(a\left(x-2\right)+b\left(y-5\right)=0\Leftrightarrow ax+by-2a-5b=0\) (1) với \(a^2+b^2>0\)
Áp dụng công thức khoảng cách:
\(d\left(I;d\right)=\dfrac{\left|a.4+b.1-2a-5b\right|}{\sqrt{a^2+b^2}}=2\)
\(\Leftrightarrow\left|2a-4b\right|=2\sqrt{a^2+b^2}\)
\(\Leftrightarrow\left|a-2b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow a^2-4ab+4b^2=a^2+b^2\)
\(\Leftrightarrow3b\left(3b-4a\right)=0\Rightarrow\left[{}\begin{matrix}b=0\\b=\dfrac{4a}{3}\end{matrix}\right.\)
Thế vào (1):
\(\Rightarrow\left[{}\begin{matrix}ax+0.y-2a-5.0=0\\ax+\dfrac{4a}{3}.y-2a-5.\dfrac{4a}{3}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\3x+4y-26=0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2022
Bài 2:
Bài này có nhiều cách làm, (ví dụ viết phương trình đường thẳng d, tính khoảng cách tới A và B rồi cho chúng bằng nhau, từ đó suy ra tương tự câu a), hoặc đơn giản hơn là lý luận như sau:
Đường thẳng d cách đều 2 điểm AB khi nó thỏa mãn 1 trong 2 trường hợp sau:
TH1: d song song AB
Ta có \(\overrightarrow{AB}=\left(-2;8\right)=2\left(-1;4\right)\Rightarrow d\) nhận (4;1) là 1 vtpt (do d song song AB)
Phương trình d có dạng:
\(4\left(x+2\right)+1\left(y-3\right)=0\Leftrightarrow4x+y+5=0\)
TH2: d đi qua trung điểm của AB
Gọi M là trung điểm AB, theo công thức trung điểm ta có \(M\left(4;3\right)\Rightarrow\overrightarrow{IM}=\left(6;0\right)=6\left(1;0\right)\)
\(\Rightarrow\) Đường thẳng d (hay IM) nhận (0;1) là 1 vtpt
Phương trình: \(0\left(x+2\right)+1\left(y-3\right)=0\Leftrightarrow y-3=0\)
5 tháng 3 2022
\(\left(x\ne3;x\ne\dfrac{1}{2}\right)\)\(\left\{{}\begin{matrix}\dfrac{2}{2x-1}\le\dfrac{1}{3-x}\\\left|x\right|< 1\Leftrightarrow-1< x< 1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2\left(3-x\right)-2x+1}{\left(2x-1\right)\left(3-x\right)}\le0\left(1\right)\\-1< x< 1\end{matrix}\right.\)\(\)
\(\left(1\right)\Leftrightarrow\dfrac{-4x+7}{\left(2x-1\right)\left(3-x\right)}\le0\)\(\Leftrightarrow\dfrac{-4x+7}{-2x^2+7x-3}\le0\Leftrightarrow x\in\left(-\infty;\dfrac{1}{2}\right)\cup[\dfrac{7}{4};3)\)
\(kết\) \(hợp:-1< x< 1\)\(\Rightarrow x\in\left(-1;\dfrac{1}{2}\right)\cup[\dfrac{7}{4};3)\)
\(b,\)\(\left(x-1\right)\left(x-4\right)\left(x-5\right)\left(x-8\right)+35>0\)
\(\Leftrightarrow\left(x^2-9x+8\right)\left(x^2-9x+20\right)+35>0\)
\(đặt:x^2-9x+8=t\ge-\dfrac{49}{4}\)
\(bpt\Leftrightarrow t\left(t+12\right)+35>0\Leftrightarrow t^2+12t+35>0\Leftrightarrow\left[{}\begin{matrix}t< -7\\t>-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-9x+8< -7\\x^2-9x+8>-5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{9-\sqrt{21}}{2}< x< \dfrac{9+\sqrt{21}}{2}\\x\in\left(-\infty;\dfrac{9-\sqrt{29}}{2}\right)\cup\left(\dfrac{9+\sqrt{29}}{2};+\infty\right)\end{matrix}\right.\)
\(c;\)\(\left(x^2+x+4\right)^2+2.4x\left(x^2+x+4\right)+16x^2-x^2>0\)
\(\Leftrightarrow\left(x^2+x+4+4x\right)^2-x^2>0\)
\(\Leftrightarrow\left(x+2\right)^2\left(x^2+6x+4\right)>0\)
\(\Leftrightarrow x^2+6x+4>0\Leftrightarrow....\)
ý d; giống ý b
\(e;bpt\Leftrightarrow\left(x-2\right)\left(x-1\right)\left(x+7\right)\left(x+8\right)+8>0\)
\(\Leftrightarrow\left(x^2+6x-16\right)\left(x^2+6x-7\right)+8>0\)
\(đặt:x^2+6x-7=t\ge-16\Rightarrow t\left(t-9\right)+8>0\)
(làm giống ý b)
\(f;x^4-2x^3+x-2>0\Leftrightarrow\left(x+1\right)\left(x-2\right)\left(x^2-x+1\right)>0\left(do:x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\right)\)
\(\Rightarrow bpt\Leftrightarrow\left(x+1\right)\left(x-2\right)>0\Leftrightarrow\left[{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\)
\(g;h\) dùng bảng phá giá trị tuyệt đối để làm
NH
0
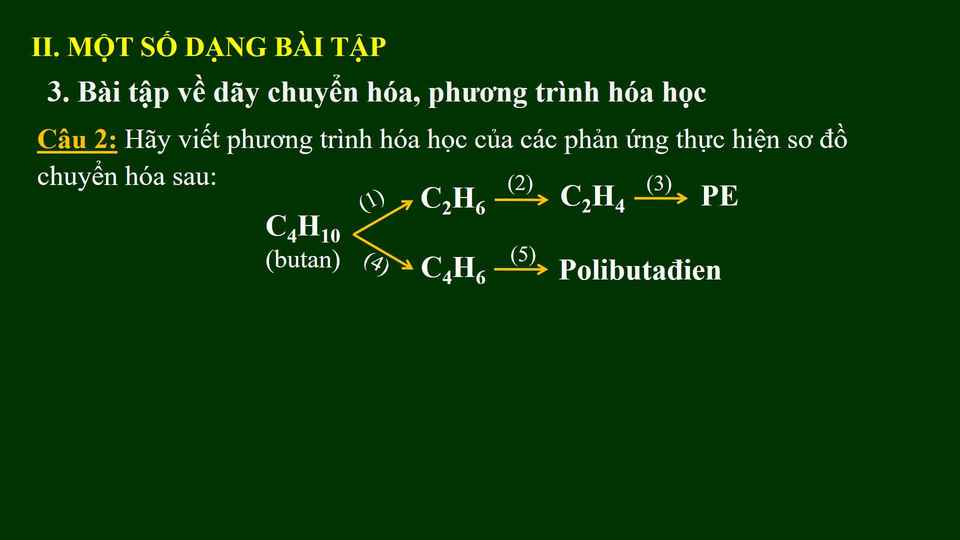
Đốt cháy các khí rồi cho sản phẩm vào dung dịch Ca(OH)2. Hiện tượng xuất hiện kết tủa vẩn đục trắng, ta sẽ nhận biết được khí etan.
Dẫn khí qua dung dịch brom (dung dịch có màu da cam). Xảy ra hiện tượng: dung dịch brom đã bị mất màu thì đó là etilen
Dẫn khí qua dung dịch brom màu da cam xảy ra hiện tượng: dung dịch brom bị mất màu.
=> đó là propin