giải hệ phương trình sau bằng phương pháp thế
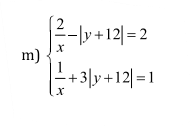
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{135}{x}-\dfrac{63}{y}=81\\\dfrac{28}{x}+\dfrac{63}{y}=245\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{163}{x}=326\\\dfrac{4}{x}+\dfrac{9}{y}=35\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\\dfrac{9}{y}=35-\dfrac{4}{x}=35-8=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)

Đáp án D
Ta có:
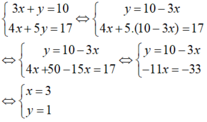
Vậy nghiệm của hệ phương trình đã cho là: (3; 1).

Ta có ( biểu diễn y theo x từ phương trình thứ hai):
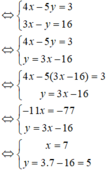
Vậy hệ phương trình có nghiệm duy nhất (7;5)

Ta có ( biểu diễn y theo x từ phương trình thứ hai):
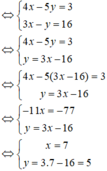
Vậy hệ phương trình có nghiệm duy nhất (7;5)

7 x - 3 y = 5 1 4 x + y = 2 2
Từ (2) rút ra được y = -4x + 2.
Thế y = -4x + 2 vào phương trình (1) ta được :
7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 ⇔ 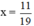
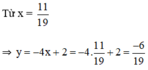
Vậy hệ phương trình có nghiệm duy nhất 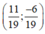

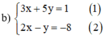
Từ (2) ta rút ra được y = 2x + 8 (*)
Thế (*) vào phương trình (1) ta được :
3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.
Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.
Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).

x + 3 y = - 2 1 5 x - 4 y = 11 2
Từ (1) rút x theo y ta được: x = -3y – 2
Thế x = -3y – 2 vào phương trình (2) ta được :
5.(-3y – 2) – 4y = 11 ⇔ -15y – 10 – 4y = 11 ⇔ -19y = 21 ⇔ 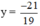
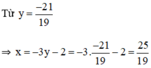
Vậy hệ phương trình có nghiệm duy nhất 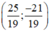

x - y = 3 3 x - 4 y = 2
Từ (1) rút ra được y = x – 3
Thế vào phương trình (2) ta được:
3x – 4.(x – 3) = 2 ⇔ 3x – 4x + 12 = 2 ⇔ x = 10
Từ x = 10 ⇒ y = x – 3 = 7.
Vậy hệ phương trình có nghiệm duy nhất (10 ; 7).