giúp mình với ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


The youth was made empty his pocket by the police
Unless it stop raining, we won't get home

- Hợp chất vô cơ: CO2, Na2CO3
- Hợp chất hữu cơ:
+ Hiđrocacbon: C4H10, C6H6, C3H4
+ Dẫn xuất của hiđrocacbon: C3H8O, CH3Cl, C6H6Cl6

11:
a: \(BD=AC=\sqrt{\left(3a\right)^2+\left(4a\right)^2}=5a\)
|vecto AB+vecto AD|
=|vecto AB+vecto BC|
=|vecto AC|
=5a
b: Gọi M là trung điểm của BC
=>BM=CM=BC/2=2a
\(AM=\sqrt{AB^2+BM^2}=a\sqrt{13}\)
Xét ΔABC có AM là trung tuyến
nên vecto AB+vecto AC=2*vecto AM
=>|vecto AB+vecto AC|=2|vecto AM|
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=2a\sqrt{13}\)


a) \(\dfrac{1}{\sqrt[]{x}-1}+\dfrac{1}{1+\sqrt[]{x}}+1\left(x\ge0;x\ne1\right)\)
\(=\dfrac{\sqrt[]{x}+1+\sqrt[]{x}-1+x-1}{\left(\sqrt[]{x}-1\right)\left(\sqrt[]{x}+1\right)}\)
\(=\dfrac{x+2\sqrt[]{x}-1}{x-1}\)
\(=\dfrac{x-1+2\sqrt[]{x}}{x-1}\)
\(=1+\dfrac{2\sqrt[]{x}}{x-1}\)
b) \(\dfrac{1}{\sqrt[]{x}+2}-\dfrac{2}{\sqrt[]{x}-2}-\dfrac{4}{4-x}\left(x\ge0;x\ne4\right)\)
\(=\dfrac{\sqrt[]{x}-2-2\left(\sqrt[]{x}+2\right)+4}{\left(\sqrt[]{x}+2\right)\left(\sqrt[]{x}-2\right)}\)
\(=\dfrac{\sqrt[]{x}-2-2\sqrt[]{x}-4+4}{\left(\sqrt[]{x}+2\right)\left(\sqrt[]{x}-2\right)}\)
\(=\dfrac{-\sqrt[]{x}-2}{\left(\sqrt[]{x}+2\right)\left(\sqrt[]{x}-2\right)}\)
\(=\dfrac{-\left(\sqrt[]{x}+2\right)}{\left(\sqrt[]{x}+2\right)\left(\sqrt[]{x}-2\right)}\)
\(=\dfrac{-1}{\sqrt[]{x}-2}\)

12:

a: Gọi M là trung điểm của BC
trên tia đối của tia MA, lấy D sao cho M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hình chữ nhật
=>\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\)
=>\(\overrightarrow{v}=\overrightarrow{AD}\)
b: \(\left|\overrightarrow{v}\right|=\left|\overrightarrow{AD}\right|=AD=2\cdot AM=2\cdot\dfrac{BC}{2}=BC=\sqrt{\left(6a\right)^2+\left(8a\right)^2}=10a\)
hình như đó đâu phải là câu 12 đâu ạ 🤔🤔🤔 trong đề câu 12 có chi tiết nào liên quan tới M đâu 🤔


Nếu có đăng nữa thì bạn viết rõ chữ ra nhé.
Cho tình huống sau :
Trên đường đến trường em nhặt được 1 túi xách có tiền và một giấy tuỳ thân mang trên Nguyễn Thị A. Để thực hiện tốt quyền sở hữu tài sản và nghĩa vụ tôn trọng tài sản của người khác, em sẽ làm gì ?
=> Trong tình huống trên , em sẽ :
- Mang đến cơ quan địa phương gần nhất để khai báo
- Không lấy số tiền đó , mà để im như cũ và tìm cách giải quyết
- Nhờ bố mẹ giúp đỡ
- Không lấy bất kì thứ gì có trong túi xách
- Khi tìm được người đánh mất chiếc túi xách này thì phải khuyên và nhắc nhở họ nên chú ý , kiểm tra xem bản thân có mất gì không .
- Và bảo họ " hạn chế mang những thứ có giá trị ra ngoài đường , nếu lỡ đâu khi bị rơi mất túi xách , thì những người xấu sẽ lạm dụng thời cơ này để lấy trộm hết thứ có giá trị "
- Chỉ mang những thứ cần thiết khi ra ngoài .
Đề : Trên đường đến trường em nhặt được 1 túi sách có tiền và 1 số giấy tờ tùy thân mang tên Nguyễn Thị A. Để thực hiện tốt quyền sở hữu tài sản và nghĩa vụ tôn trọng tài sản của người khác, em sẽ làm gì?
Để thực hiện tốt quyền sở hữu tài sản và nghĩa vụ tôn trọng của người khác, em sẽ:
- Em sẽ mang túi sách đến đồn công an
- Nhờ người lớn giúp đỡ.
- Không mở ra lục lọi, soi mói hay lấy bất cứ thứ gì trong túi sách
- ....
*NẾU người làm mất có gửi tiền cho em để hậu tạ thì em sẽ từ chối, vì làm việc tốt đâu để được khen hay thưởng. Khi giúp đỡ mọi người, trong lòng mình thấy vui và giúp được người khác thành công đã là món quà vô cùng ý nghĩa rồi.*


22:
a:
\(\overrightarrow{AD}=2\overrightarrow{DB}\)
=>\(\overrightarrow{AD}=\dfrac{2}{3}\overrightarrow{AB}\)
\(\overrightarrow{CE}=3\overrightarrow{EA}\)
=>\(\overrightarrow{AE}=\dfrac{1}{3}\overrightarrow{EC}\)
=>\(\overrightarrow{AE}=\dfrac{1}{4}\overrightarrow{AC}\)
Xét ΔAED có AM là trung tuyến
nên \(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{AE}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{8}\overrightarrow{AC}\)
b: \(\overrightarrow{MI}=\overrightarrow{ME}+\overrightarrow{EI}\)
\(=\dfrac{1}{2}\overrightarrow{DE}+\overrightarrow{EC}+\overrightarrow{CI}\)
\(=\dfrac{1}{2}\left(\overrightarrow{DA}+\overrightarrow{AE}\right)+\dfrac{3}{4}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CB}\)
\(=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)+\dfrac{3}{4}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CA}+\dfrac{1}{2}\overrightarrow{AB}\)
\(=\dfrac{-1}{3}\overrightarrow{AB}+\dfrac{1}{8}\overrightarrow{AC}+\dfrac{3}{4}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AB}\)
\(=\dfrac{1}{6}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}\)

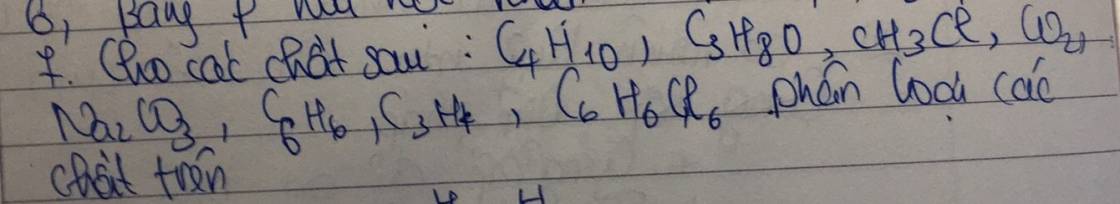


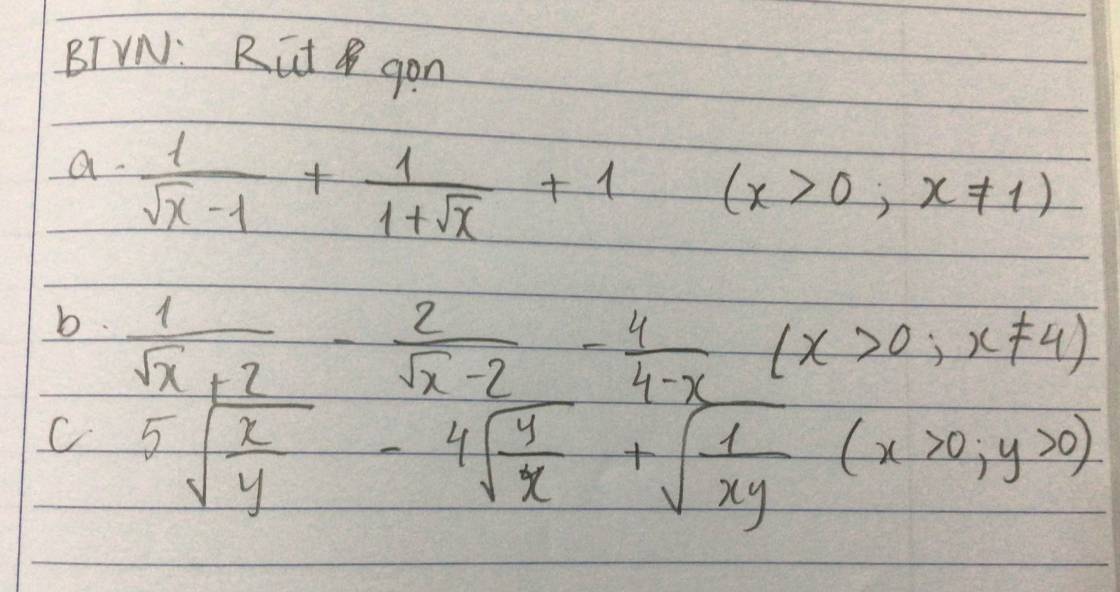
 Mọi người giúp mình với ạ, mình đang gì cần gấp, giúp mình nhé😭😭
Mọi người giúp mình với ạ, mình đang gì cần gấp, giúp mình nhé😭😭

