cho tam giác abc cân tại a. trên tia đối bc lấy d. trên tia đối cb lấy e sao cho cd=be. a) chứng minh góc adb = góc ace
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
29 tháng 12 2020
a) Ta có:
OC = OA + AC
OD = OB + BD
Mà OA = OB (gt)
AC = BD (gt)
\(\Rightarrow\) OC = OD
Xét \(\Delta OAD\) và \(\Delta OBC\) có:
\(\widehat{O}\) chung
OA = OB (gt)
OD = OC (cmt)
\(\Rightarrow\Delta OAD=\Delta OBC\) (c-g-c)
\(\Rightarrow AD=BC\) (hai cạnh tương ứng)
KV
29 tháng 12 2020
b) Do \(\Delta OAD=\Delta OBC\) (cmt)
\(\Rightarrow\widehat{BDE}=\widehat{ACE}\) (hai góc tương ứng)
\(\widehat{OAD}=\widehat{OBC}\) (hai góc tương ứng)
Mà \(\widehat{EAC}+\widehat{OAD}=180^0\) (kề bù)
\(\widehat{EBD}+\widehat{OBC}=180^0\) (kề bù)
\(\Rightarrow\widehat{EAC}=\widehat{EBD}\)
Xét \(\Delta EAC\) và \(\Delta EBD\) có:
\(\widehat{EAC}=\widehat{EBD}\) (cmt)
AC = BC (gt)
\(\widehat{ACE}=\widehat{BDE}\) (cmt)
\(\Rightarrow\Delta EAC=\Delta EBD\) (g-c-g)
30 tháng 6 2023
a: ΔABC cân tại A nên góc ABC<90 độ
=>góc ABD>90 độ
=>AB<AD
b: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
c: MB+BD=MD
MC+CE=ME
mà MB=MC và BD=CE
nên MD=ME
=>M là trung điểm của DE
=>AM là đường trung tuyến của ΔADE
d: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
=>ΔAHB=ΔAKC
=>HB=KC
f: Xét ΔADE có AH/AD=AK/AE
nên HK//DE
18 tháng 12 2021
a: Xét ΔBAD và ΔCAD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
30 tháng 3 2023
a: Xet ΔCBD có
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
=>CA là phân giác củagóc BCD
b: Xét ΔCEI vuông tại E và ΔCFI vuông tại F có
CI chung
góc ECI=góc FCI
=>ΔCEI=ΔCFI
=>CE=CF
=>ΔCEF cân tạiC
Xet ΔCDB có CE/CD=CF/CB
nên EF//DB
c: IE=IF
IF<IB
=>IE<IB
8 tháng 12 2021
a: Xét ΔAHB vuông tại H và ΔAHK vuông tại H có
AH chung
HB=HK
Do đó: ΔAHB=ΔAHK
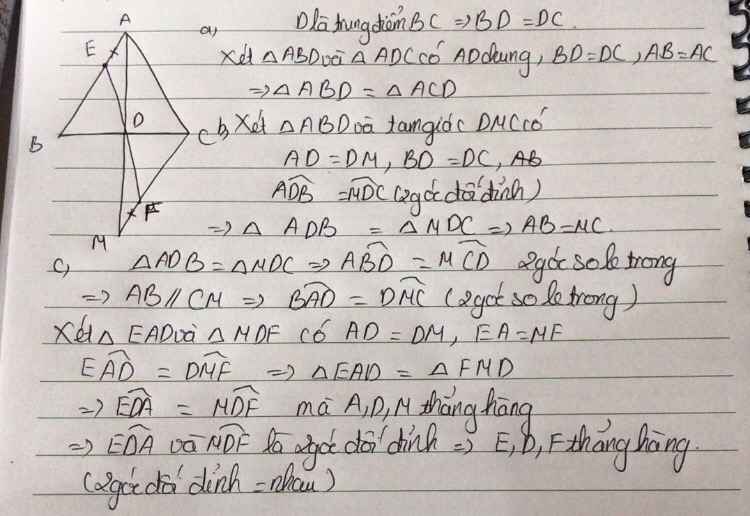
Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: \(\widehat{ADB}=\widehat{AEC}\)